Théorème de Pythagore

Théorème de Pythagore

Théorème de Pythagore

I – Théorème de Pythagore direct :

1/ Activité 1 :

ABC un triangle tel que AB = 3 \; cm et AC = 4 \; cm et BC = 5 \; cm

  1. a. Construire le triangle ABC
    b. Que remarquez vous sur la nature du triangle ABC
  2. Vérifiez que BC^2 = AB^2 + AC^2

Réponse :

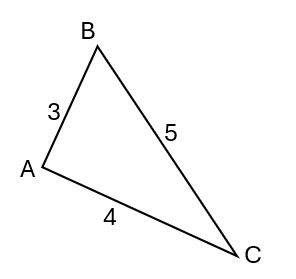
  1. a. La figure : activité théorème de Pythagoreb. En utilisant l’équerre, on trouve que le triangle ABC est rectangle en A.
  2. On a AB^2 + AC^2 = 3^2 + 4^2 = 9 + 16 = 25
    et BC^2 = 5^2 = 25
    Donc BC^2 = AB^2 + AC^2

2/ Théorème de Pythagore direct :

a- Propriété 1 :

Dans un triangle rectangle, le carré de son hypoténuse est égale à la somme des carrés des longueurs des côtés de l’angle droite.

Autrement dit : Si ABC est un triangle rectangle en A Alors :

BC^2 = AB^2 + AC^2

b- Figure géométrique :

ABC est un triangle rectangle en A:

figure géométrique Pythagore

Donc BC^2 = AB^2 + AC^2

c- Remarques :

ABC est un triangle rectangle en A,

Donc BC^2 = AB^2 + AC^2

Alors \left\{\begin{array}{l}\;\;\;AB^2 = BC^2 - AC^2 \\ \;\;\; AC^2 = BC^2 - AB^2 \end{array}\right.

On utilise le théorème de Pythagore pour calculer les longueurs.

d- Exemples :

EFG un triangle rectangle en E, tel que :

EF = 5 \; cm et EG = 3 \; cm

Calculer FG.

⇒ On a EFG un triangle rectangle en E, Donc d’après de théorème de Pythagore direct on a :

FG^2 = EF^2 + EG^2\\ FG^2 = 5^2 + 3^2\\ FG^2 = 25 + 9\\ FG^2 = 34\\

D’où FG^2 = \sqrt{34}

2/ Exercice d’application :

ABC un triangle isocèle et rectangle en A tel que AB = 4 \; cm

Soit M le milieu de [BC]

  1. Construire la figure.
  2. Calculer BC.
  3. Déduire AM.

II – Théorème réciproque de Pythagore :

1/ Activité 2 :

ABC un triangle tel que AB = 4 \; cm et AC = 3 \; cm et BC = 5 \; cm

  1. Comparer BC^2 et AB^2 + AC^2
  2. Construire le triangle ABC
  3. Quelle est la nature du triangle ABC ?
  4. Quelle est la propriété qu’on peut extraire ?

Solution :

  1. On a AB^2 + AC^2 = 3^2 + 4^2 = 9 + 16 = 25 et BC^2 = 25
    Donc AB^2 + AC^2 = BC^2
  2. La figure :activité théorème réciproque de Pythagore
  3. En utilisant l’équerre, on trouve que le triangle ABC est rectangle en A.
  4. On a trouvé que si ABC est un triangle tel que BC^2 = AB^2 + AC^2 Alors ABC est un triangle rectangle en A.

2/ Théorème réciproque de Pythagore :

a- Propriété 2 :

Dans un triangle, si le carré de la longueur du plus grand côté est égale à la somme des carrées des longueurs des deux autres côtés, alors de triangle est rectangle.

Autrement dit : Si dans un triangle ABC, on a BC^2 = AB^2 + AC^2, Alors ce triangle est rectangle en A.

b- Figure géométrique :

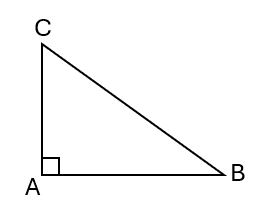
figure géométrique Pythagore réciproque

ABC un triangle tel que BC^2 = AB^2 + AC^2

Alors ABC est triangle rectange en A

c- Remarque :

On utilise le théorème de Pythagore réciproque pour montrer qu’un triangle est rectangle (pour montrer la perpendicularité).

d- Exemple :

EFG un triangle tel que :

EG = 6 \; cm et FG = 8 \; cm et EF = 10 \; cm

Montrons que EFG est un triangle rectangle en G.

Solution :

On a \left \{ \begin{array}{r c l} EG^2 & = & 6^2 & = & 36\\ FG^2 & = & 8^2 & = & 64 \\ EF^2 & = & 10^2 & = & 100 \end{array} \right .

Donc EG^2 + FG^2 = 36 + 64 = 100

Alors EG^2 + FG^2 = EF^2

Donc d’après le théorème de Pythagore réciproque, le triangle EFG est rectangle en G.

3/ Exercice d’application :

Soit ABC un triangle tel que :

AB = 2\sqrt2 \; cm, AC = \sqrt3 \; cm et BC = \sqrt5 \; cm

Montrer que ABC est un triangle rectangle.