Système de deux équations du premier degré à deux inconnues

Système de deux équations du premier degré à deux inconnues

Système de deux équations du premier degré à deux inconnues

I – Système de deux équations du premier degré à deux inconnues :

1/ Définition :

Soient a, a', b, b', c et c' nombres réels.On a appelle système de deux équations du premier degré à deux inconnues, toute écriture de la forme :\left\{\begin{array}{l} ax + by = c \\ a'x + b'y = c' \end{array}\right.\\

d’inconnues x et y

2/ Exemples :

On considère les systèmes suivants :

\left\{\begin{array}{l} 3x - 2y = 5 \\ x + 2y = 3 \end{array}\right. et \left\{\begin{array}{l} \frac{1}{2}x - 3y - \frac{2}{3} = 0 \\ -3x + y + 2 = 0 \end{array}\right.

I – La résolution des systèmes :

1/ Définition :

Résoudre un système, c’est trouver tous les couples (x,y)(s’il existent) pour lesquels les deux équations sont vérifiées simultanément.La résolution des systèmes se divise en deux poste :

  • La résolution algébrique : on a deux méthodes
    • Méthode par substitution
    • Méthode de combinaison linéaire
  • La résolution graphique

2/ La résolution algébrique d’un système :

a- Méthode de substitution :

⇒ Définition :
Cette méthode consiste à exprimer l’un des inconnues en fonction de l’autre dans une des équations, et la remplacer dans l’autre équation pour trouver une équation à une inconnue.
⇒ Remarque :

On utilise de préférence la méthode par substitution lorsque l’une des deux inconnues a pour coefficient 1 ou -1

⇒ Exemple :

Résoudre le système \left\{\begin{array}{l} 3x + y = 11 \\ x + 3y = 18 \end{array}\right. (S)

→ Dans l’équation 1, on écrit y en fonction de x

Donc y = 11 - 2x

→ On substitue y dans l’équation 2, on trouve : x + 3(11 - 2x) = 18
x + 33 - 6x = 18-5x = 18 - 33-5x = -15x = \frac{-15}{-5}x = 3
→ On remplace x par 3 dans l’équation 3 :
y = 11 - 2 \times 3 = 11 - 6 = 5
Donc le couple (3;5) est la solution du système (S)

b- Méthode de combinaison linéaire :

⇒ Définition :
Cette méthode consiste à multiplier chaque équation du système par un nombre convenable pour obtenir deux coefficients opposés pour la même inconnue. Ensuite, on additionne les deux équations trouvées, membre à membre, afin d’obtenir une équation du premier degré à une inconnue.
⇒ Remarque :

On utilise de préférence la méthode de combinaison linéaire si on a deux termes opposés pour la même inconnue.

⇒ Exemple :

Résolvons le système \left\{\begin{array}{l} (1) -5x + 4y = -1 \\ (2) 3x - 2y = 1 \end{array}\right.

∗ Elimination de y

→ On multiplie les membres de l’équation (2) par 2

Donc \left\{\begin{array}{l} -5x + 4y = -1 \\ 6x - 4y = 2 \end{array}\right.

→ On ajoute ces équations membre à membre
-5x + 4y + 6x - 4y = -1 + 2x = 1
∗ Elimination de x

→ On multiplie les membres de l’équation (1) par 3 et les membres de l’équation (2) par 5
\left\{\begin{array}{l} -15x + 12y = -3 \\ 15x - 10y = 5 \end{array}\right.
→ On ajoute ces équations membre à membre
-15x + 12y + 15x -10y = -3 + 52y = 2y = \frac{2}{2}y = 1
Donc le couple (1;1) est la solution du système

∗ Technique 2 :

Dans l’étape 2, au lieu d’éliminer x par la combinaison linéaire, on remplace juste dans l’une des équations.

On a : x = 1

On remplace dans l’équation (2) :
3 \times 1 - 2y = 13 - 2y = 1-2y = 1 - 3-2y = -2y = \frac{-2}{-2} = 1
On trouve donc le même couple (1;1)

⇒ Remarque :

On doit respecter la méthode demandé par l’exercice.

3/ La résolution graphique :

a- Définition :

Cette méthode consiste à lier chaque équation du système par une droite, et déterminer le couple  de coordonnées de leur point d’intersection (s’ils se coupent), cela dans un repère orthonormé, alors ce couple est la solution du système.

b- Exemple 1 :

Résolvons le système (S) \left\{\begin{array}{l} 4x - y - 2 = 0 \\ 2x - y + 2 = 0 \end{array}\right.

→ Pas 1 : Trouver les équations réduites :

On a : 4x - y - 2 = 0 Donc y = 4x - 2

On a : 2x - y + 2 = 0 Donc y = 2x + 2

On considère les deux droites (D)_{1} et (D)_{2} tel que :
\left\{\begin{array}{l} (D)_{1} : y = 4x - 2 \\ (D)_{2} : y = 2x + 2 \end{array}\right.
On remarque que les deux droites (D)_{1} et (D)_{2} n’ont pas la même pente, donc elles sont sécantes.

→ Pas 2 : la représentation des droites (D)_{1} et (D)_{2} :

(D)_{1}

x 0 1
y 2 4
M(x;y) E(0;2) F(1;4)

 

(D)_{0}

x 0 1
y -2 2
M(x;y) A(0;-2) B(1;2)

On remarque que les deux droites (D)_{1} et (D)_{2} se coupent au point M(2;6)

Pas 2 présentation graphique

⇒ Alors le couple (2;6) est la solution du système.

c- Exemple 2 :

Résolvons : \left\{\begin{array}{l} 2x + y - 1 = 0 \\ 4x + 2y = 2 \end{array}\right.

On considère les droites (D) et (Δ) telle que :

(D) : 2x + y - 1 = 0 et (Δ) : 4x + 2y = 2

Cherchons les équations réduites des droites (D) et (Δ)

On a \left\{\begin{array}{l} 2x + y - 1 = 0 \\ 4x + 2y = 2 \end{array}\right. Donc \left\{\begin{array}{l} y = -2x + 1 \\ 2y = -4x + 2 \end{array}\right.\\
\left\{\begin{array}{l} y = -2x + 1 \\ y = \frac{-4x + 2}{2} = -2x + 2 \end{array}\right.\\
Alors : \left\{\begin{array}{l} (D) : y = -2x + 2 \\ (Δ) : y = -2x + 1 \end{array}\right.

On remarque que les deux droites (D) et (Δ) ont la même équation réduite.

Donc (D) et (Δ) sont deux droites confondues.

Alors le système admet une infinité de solutions (x;y)

d- Exemple 3 :

Résolvons : \left\{\begin{array}{l} 3x + y - 5 = 0 \\ 6x + 2y + 1 = 0 \end{array}\right.

On considère les droites (D) et (Δ) telle que :

(D) : 3x + y - 5 = 0 et (Δ) : 6x + 2y + 1 = 0

Cherchons les équations réduites des droites (D) et (Δ)

On a \left\{\begin{array}{l} 3x + y - 5 = 0 \\ 6x + 2y + 1 = 0 \end{array}\right. Donc \left\{\begin{array}{l} y = -3x + 5 \\ 2y = -6x - 1 \end{array}\right.\\
y = -3x + 5y = \frac{-6x + 1}{2} = -3x + \frac{1}{2}
Alors \left\{\begin{array}{l} (D) : y = -3x + 5 \\ (Δ) : y = -3x + \frac{1}{2} \end{array}\right.

On remarque que les deux droites (D) et (Δ) ont la même pente (mais pas la même ordonnée à l’origine)

Donc : (D) et (Δ) sont strictement parallèles.

D’où ce système n’admet pas de solutions.

e- Propriété récapitulatif  :

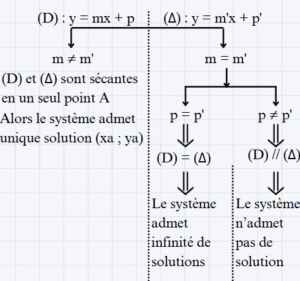
On considère les deux droites :

(D) : y = mx + p et (Δ) : y = m'x + p'

propriété recapitulatif

III – Systèmes et problèmes :

1/ Règle :

La résolution d’un problème déroule en 4 étapes :

  1. Choix des inconnues : Trouvés à la question.
  2. Mise en système : Transformation des données en équations.
  3. Résolution du système : algébriquement.
  4. Retour au problème : Vérification de la solution et réponse à la question.

2/ Exemple :

Une usine fabrique deux sortes d’objets : A et B.

L’objet A nécessite 2\;kg d’acier et 3 heures de fabrication.

L’objet B nécessite 4\;kg d’acier et 2 heures de fabrication.

Combien d’objet de chaque sorte a-t-on fabriqué en 68 heures de travail en utilisant 80\;kg d’acier ?

Solution :

  1. Choix des inconnues :
    Soient x le nombre d’objet A
    y le nombre d’objet B
  2. Mise en système :
    Puisque l’objet A nécessite 2\;kg d’acier et l’objet B nécessite 4\;kg
    Alors : l’ensemble d’objets fabriqués utilisant 80\;kg d’acier : 2x + 4y = 80
    ∗ Puisque l’objetA nécessite 3 heures de fabrication et que l’objet B nécessite 2 heures de fabrication
    Alors : l’ensemble d’objets fabriqués utilisant 68 heures est : 3x + 2y = 68
    D’où le système est : \left\{\begin{array}{l} 2x + 4y = 80 \\ 3x + 2y = 68 \end{array}\right.
  3. Résolution du système :
    On a : \left\{\begin{array}{l} (1) : 2x + 4y = 80 \\ (2) : 3x + 2y = 68 \end{array}\right.\\
    On multiplie l’équation (2) par -2
    Donc \left\{\begin{array}{l} (1) : 2x + 4y = 80 \\ (2) : -6x - 4y = -136 \end{array}\right.\\
    On ajoute les équations membre à membre
    2x + 4y - 6y - 4y = 80 - 136
    -4x = -56
    x = \frac{-56}{-4} = 14
    On remplace dans l’équation (1), donc
    2 \times 14 + 4y = 80
    28 + 4y = 80
    4y = 80 - 28
    4y = 52
    y = \frac{52}{4} = 13
    D’où le système admet pour unique solution le couple (14;13)
  4. Retour au problème :
    On a \left\{\begin{array}{l} 2 \times 14 + 4 \times 13 = 28 + 52 = 80 \\ 3 \times 14 + 2 \times 13 = 42 + 26 = 68\end{array}\right.
    Alors :
    Le nombre d’objet A fabriqués est : 14
    Le nombre d’objet B fabriqués est : 13