Géométrie dans l’espace
Géométrie dans l’espace
I – Orthogonalité d’une droite et d’un plan :
1/ Définition :
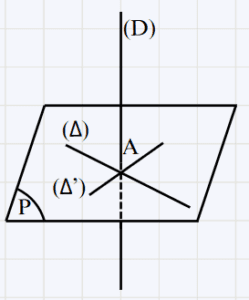
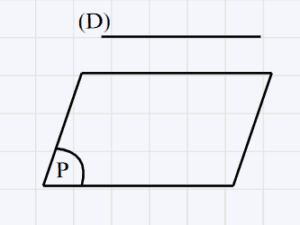
∗ Figure géométrique :
∗ On a : (D) \perp (Δ) et (D) \perp (Δ ') au point A
∗ On a : (Δ) \perp (Δ ') sont inclus dans (P) alors (D) \perp (P)
∗ Exemple :
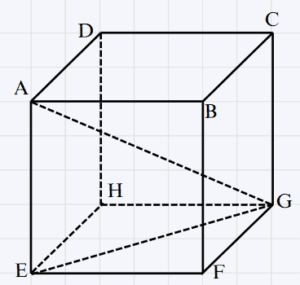
ABCDEFGH un cube.
Montrons que (AE) \perp (EFGH)
On a ABEF et ADHF deux carrés, donc :
∗ (AE) \perp (EH) en E
∗ (AE) \perp (EF) en E
∗ (EF) et (EH) sont inclus dans le plan (EFGH) et se coupent en E
Alors d’après la définition (AE) \perp (EFGH) en E
2/ Propriété 1 :
a- Propriété 1 :
b- Exemple :
On considère le cube ABCDEFGH précédent
Montrons que le triangle AEG est rectangle en E.
On a (AE) \perp (EFGH) en E
Comme la droite (EG) et passe par E
Donc d’après la propriété 1 : (AE) \perp (EG)
Cela signifie que le triangle AEG est rectangle en E
3/ Théorème de Pythagore dans l’espace :
a- Théorème de Pythagore directe :
∗ Exemple :
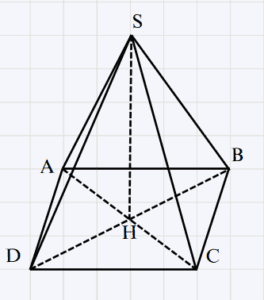
La figure représente un pyramide régulier SABCD à base carré ABCD et de hauteur [SH] tel que :
AC = BD = 12 \; cm et SH = 12 \; cm
Calcul de BC
⇒ Calcul de BC
ABCD est un carré donc le triangle ABC est rectangle en B.
Donc d’après le théorème de Pythagore directe, On a : BC^2 + AB^2 : AC^2\\
BC^2 + BC^2 = AC^2 car (AB = BC (ABCD \;carré))
2BC^2 = AC^2\\ 2BC^2 = 12^2\\ BC^2 = \frac{144}{2} = 72\\ BC = \sqrt{72} = \sqrt{6^2 \times 2} = 6\sqrt2\\⇒ Calcul de SC
On a [SH] hauteur de pyramide SABCD
Donc (SH) \perp (ABCD) en H or (HC) ⊂ (ABCD)
Alors : (SH) \perp (HC)
Donc le triangle SHC est rectangle en H
Donc d’après le théorème de Pythagore directe :
SH^2 + HC^2 = SC^2\\SC^2 = 12^2 + 6^2 car HC = \frac{AC}{2}
SC^2 = 144 + 36\\ SC^2 = 180\\ SC = \sqrt{180} = \sqrt{6^2 + 5}\\Alors SC = 6\sqrt{5}
b- Théorème de Pythagore réciproque :
∗ Exemple :
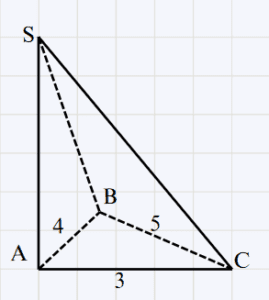
SABC tétraèdre à base le triangle ABC
tel que :
AC = 3 \;cm et AB = 4 \; cm et BC = 5 \; cm
Montrons que le triangle ABC est rectangle en A
On a AB^2 + AC^2 = 4^2 + 3^2 = 16 + 9 = 25\\
BC^2 = 5^2 = 25\\Donc AB^2 + AC^2 = BC^2\\
Alors d’après le théorème de Pythagore réciproque, le triangle ABC est rectangle en A.
II – Parallélisme d’une droite et d’un plan :
1/ Définition :
∗ Figure géométrique :
(D) ⊂ (P) ⇒ (D) // (P)
(D) // (P) car sens points communs
2/ Propriété 2 :
a- Propriété 2 :
∗ Exemple :
∗ (Δ) ⊂ (P) \; ((Δ) \; inclus \; dans \; (P))\\
∗ (Δ) // (D)
Alors (D) // (P)
b- Exemple :
ABCDEFGH parallélépipède
Montrons que : (AB) // (EFGH)
⇒ On a ABEF rectangle, donc : (AB) // (EF) et (EF) ⊂ (EFGH)\\
Donc d’après la propriété 2 : (AB) // (EFGH)\\
c- Exercice d’application :
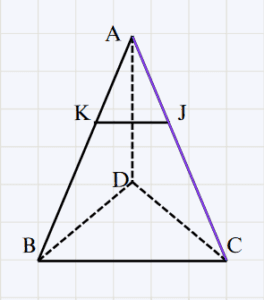
ABCD tétraèdre
J milieu de [AB], K milieu de [AD]\\
Montrons que : (JK) // (BCD)
3/ Théorème de Thalès dans l’espace :
a- propriété directe :
∗ Exemple :
On considère le pyramide ABCD tel que :
(KJ) // (BC) et AK = 2 et AB = 6 et BC = 9\\
Calculer KJ
On considère le triangle ABC
On a : \left\{\begin{array}{l}\;\;\;K ∈ [AB] \\ \;\;\; J ∈ [AC] \end{array}\right. tel que : (KJ)//(BC)\\
Donc d’après le théorème de Thalès direct on a :
\frac{AK}{AB} = \frac{AJ}{AC} = \frac{KJ}{BC}\\ \frac{AK}{AB} = \frac{KJ}{BC}\\ \frac{2}{6} = \frac{KJ}{9}\\ KJ =\frac{2 \times 9}{3} = \frac{18}{6}\\Alors : KJ = 3
a- propriété réciproque :
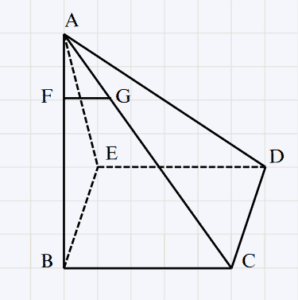
On considère la figure tel que :
AF = 3 et AB = 9 et AG = 9 et AC = 12\\
Montrer que (FG) // (BC)\\
On a :
∗ \frac{AF}{AB} = \frac{3}{9} = \frac{1}{3}\\
∗ \frac{AG}{AC} = \frac{4}{12} = \frac{1}{3}\\
Donc \frac{AF}{AB} = \frac{AG}{AC}\\
On considère le triangle ABC\\
On a : \left\{\begin{array}{l}\;\;\;F ∈ [AB] \\ \;\;\; G ∈ [AC] \end{array}\right. et les points A, F et B ont même ordre que les points A, G et C\\
Et on a : \frac{AF}{AB} = \frac{AG}{AC}\\
Donc d’après le théorème de Thalès réciproque on a : (FG) // (BC)
III – Agrandissement et réduction :
1/ Définition :
On dit qu’une figure est un agrandissement ou un réduction d’une autre figure lorsque leurs longueurs sont proportionnelles de rapport k.C’est à dire on obtient le deuxième solide en multipliant les arêtes du premier par le nombre positif non nul k (k ≠ 1)\\
k est appelé coefficient d’agrandissement ou de réduction.
2/ Remarques importantes :
∗ Si k > 1, il s’agit d’un agrandissement.
∗ Si 0 < k < 1, il s’agit d’une réduction.
∗ Si k est le coefficient d’agrandissement alors le rapport de réduction est \frac{1}{K}
3/ L’influence de l’agrandissement ou la réduction sur les aires et les volumes :
a- propriété :
→ Les aires sont multipliées par K^2
→ Les volumes sont multipliées par K^3
∗ Autrement dit :
l : longueur
A : aire
V : volume
b- Exemple :
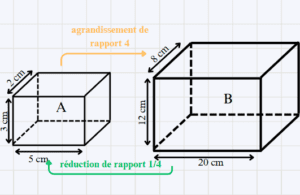
La parallélépipède B est agrandissement du parallélépipède A de rapport d’agrandissement est 4 (car les longueurs sont multipliés par 4)
⇒ et A est réduction de B de rapport \frac{1}{4}
∗ L’aire de A est :
A = 2(ab + ac + bc) = 2(5 \times 3 + 5 \times 2 + 3 \times 2) = 2 \times 31\\ A = 62 \;cm^2\\Alors l’aire de B est :
A' = k^2 \times A = 4^2 \times 62\\ A' = 992 \; cm^2∗ Le volume de A est :
V = a \times b \times c = 5 \times 3 \times 2 = 30\; cm^3\\Donc le volume de B est :
V' = k^3 \times V = 4^3 \times 30 = 1920\; cm^3∗ Remarque
Des fois, pour déterminer le rapport d’agrandissement ou de réduction, on emploie le théorème directe.
4/ Exercice d’application :
La figure ci dessous représente un pyramide régulier à base carré ABCD et de hauteur SO
tel que : BC = 6 \;cm et SO = 4 \;cm\\
I,J,K et L sont respectivement les milieu de [SA], [SB], [SC] et [SD] tel que :
SI = SJ = SK = SL = \frac{1}{3}SA\\-
- Montrer que : latex]IJ = 2 \;cm[/latex]
- Sachant que le pyramide latex]SABCD[/latex] est un agrandissement du pyramide SIJKL
- a) Déterminer son coefficient
- b) Calculer l’air du carré ABCD et déduire l’air du carré IJKL
- Calculer le volume du pyramide SABCD et déduire le volume du pyramide SIJKL
- Déduire le volume V du solide ABCDIJKL