Correction Examen Régional Mathématiques 2024 - 3APIC Tanger Tetouan Al Hoceima

Correction Examen Régional Mathématiques 2024 – 3APIC Tanger Tetouan Al Hoceima

Vous retrouvez sur cette page la Correction Examen Régional Mathématiques 2024 – 3APIC Tanger Tetouan Al Hoceima, disponible en PDF et en vidéo. Préparez-vous bien et nous vous souhaitons la réussite !

Sujet de l’examen

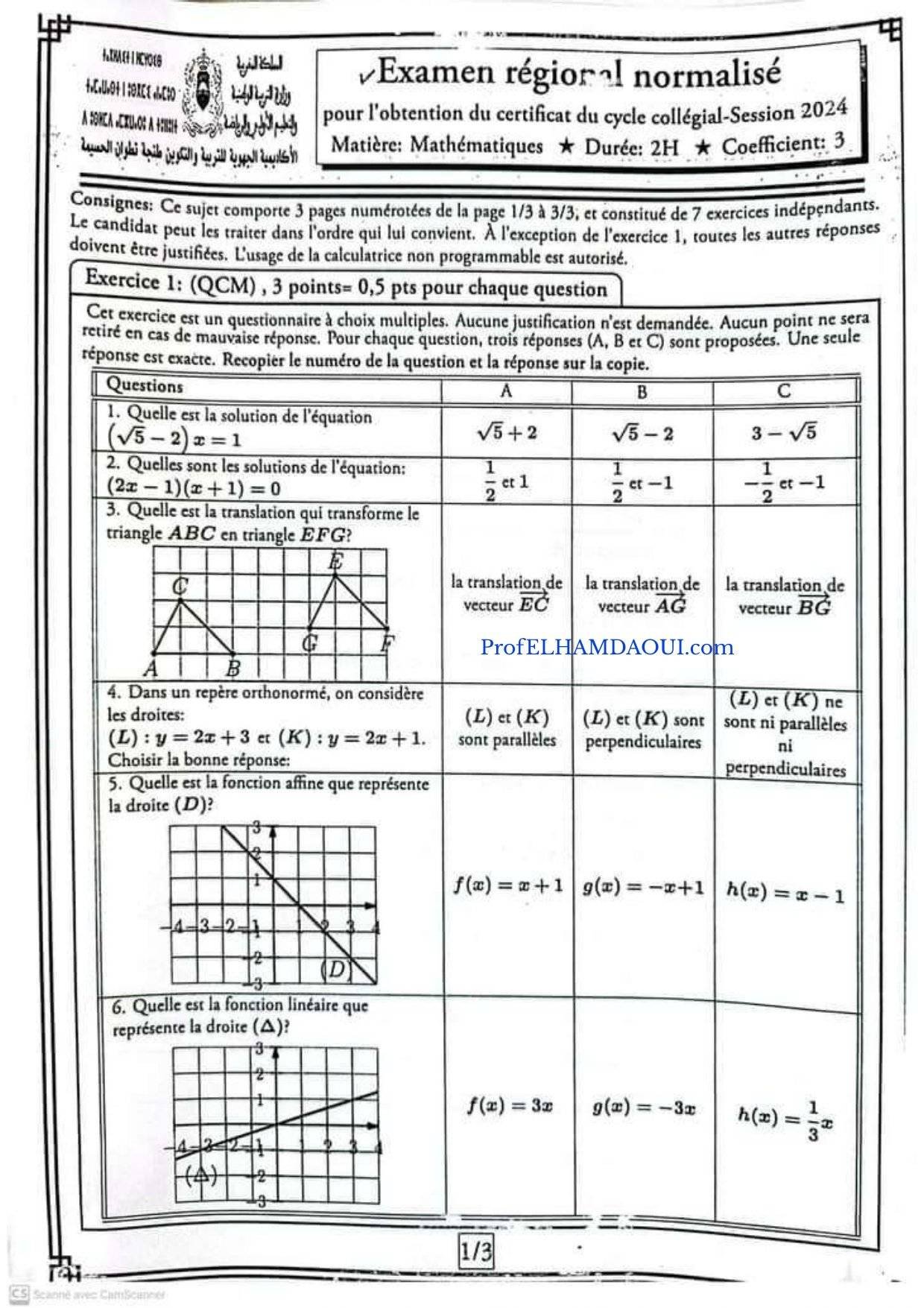
Le sujet en image :

Télécharger le sujet en PDF

La correction

Exercice 1 (QCM)

Exercice 2

Le plus grand effectif est 6 associé à la valeur 5, donc le mode est : 5
La moyenne est :
$M = \frac{(1\times3) + (2\times5) + (5\times6) + (8\times3) + (10\times3) + (11\times2) + (12\times3)}{25}\\$ $M = \frac{3+10+30+24+30+22+36}{25} = \frac{155}{25} = 6.2$
Effectifs Cumulés 3 8 14 17 20 22 25
Le pourcentage est :
$P = \frac{3+5+6+3}{25} \times 100\\$ $P = \frac{17}{25} \times 100 = 68\%$

Exercice 3

$E$ est l’image de $C$ par la translation $\overrightarrow{AD}$ , c’est-à-dire que les deux vecteurs $\overrightarrow{CE}$ et $\overrightarrow{AD}$ sont de même sens, même direction et même norme.

Autrement dit :

Le quadrilatère $ACED$ est un parallélogramme donc : $\overrightarrow{AD} = \overrightarrow{BC} \quad (1)\\$

D’après la question 1, on a :
$\overrightarrow{AD} = \overrightarrow{CE} \quad (2)\\$
De (1) et (2), on déduit que :
$\overrightarrow{BC} = \overrightarrow{CE}\\$
Ainsi, $E$ est l’image de $C$ par la translation de vecteur $\overrightarrow{BC}\\$

Exercice 4

Le volume de (P) est :
$V = \frac{S \times h}{3} = \frac{12 \times 4}{3} = \frac{4 \times 3 \times 4}{3} = 16 \text{ cm}^3$
[/latex](Q)[/latex] est la réduction de $(P)$ , alors :
$V' = (\frac{1}{2})^3 \times V = \frac{1}{8} \times 16 = 2{ cm}^3$
L’aire de $(Q)$ est :
$A' = \left(\frac{1}{2}\right)^2 \times A = \frac{1}{4} \times 12 = 3 \text{ cm}^2$

Exercice 5

Résoudre $2x - 2 = -x + 4\\$
$2x + x = 4 + 2\\$
$3x = 6\\$
$x = \frac{6}{3} = 2\\$
La solution de l’équation est $2$ .
Résoudre $-7x - 8 < 3x + 12\\$
$-7x - 3x < 12 + 8\\$
$-10x < 20\\$
$x > \frac{-20}{10} = -2\\$
Les solutions de l’inéquation sont tous les nombres réels supérieurs strictement à -2.
a) Résoudre $x^2 = 4x\\$
$x^2 - 4x = 0\\$
$x(x - 4) = 0\\$
$x = 0 \text{ ou } x - 4 = 0\\$
$x = 0 \text{ ou } x = 4\\$
Les solutions de l’équation sont 0 et 4.
b) La valeur de a pour que le périmètre du carré soit égal à son aire est :
$\text{Périmètre du carré} : 4a\\$
$\text{Son Aire} : a^2\\$
$a^2 = 4a \Rightarrow a^2 - 4a = 0\\$
D’après la question 3) a), les solutions de cette équation sont :
$a = 0 \text{ ou } a = 4\\$
Puisque $a > 0\\$
D’après les données alors la valeur de $a$ est : 4
a) Résoudre le système :
$\left\{\begin{array}{l}\;\;\;x - 2y &= -30 \quad (1) \\ \;\;\; x - y &= 36 \quad (2) \end{array}\right.\\$
En multipliant l’équation (1) par (-1), on obtient :
$\left\{\begin{array}{l}\;\;\;-x + 2y &= 30 \\ \;\;\; x - y &= 36 \end{array}\right.\\$
En ajoutant les deux équations :
$\left\{\begin{array}{l}\;\;\; -x + x + 2y - y &= 30 + 36 \\ \;\;\; y &= 66 \end{array}\right.\\$
En remplaçant y = 66 dans l’équation (2) :
$x - 66 = 36\\$
$x = 36 + 66\\$
$x = 102\\$
Le couple (102; 66) est la solution de ce système.
b) Résoudre le problème :
– Choix de l’inconnu :
$x$ : la somme d’argent de Mohamed
$y$ : la somme d’argent de Ali
– Mise en situation :
$\left\{\begin{array}{l}\;\;\; x + 10 &= 2(y - 10) \\ \;\;\; x - 18 &= y + 18 \end{array}\right.\\$
$\left\{\begin{array}{l}\;\;\; x + 10 &= 2y - 20 \\ \;\;\; x - y &= 18 + 18 \end{array}\right.\\$
$\left\{\begin{array}{l}\;\;\; x - 2y &= -20 - 10 \\ \;\;\; x - y &= 36 \end{array}\right.\\$
$\left\{\begin{array}{l}\;\;\; x - 2y &= -30 \\ \;\;\; x - y &= 36 \end{array}\right.\\$
– Résolution du système :
D’après la question 4) a), le couple (102;66) est la solution de système.
– Vérification et interprétation :
$\left\{\begin{array}{l}\;\;\; 102 + 10 &= 2(66 - 10) \\ \;\;\; 102 - 18 &= 66 + 18 \end{array}\right.\\$
$\left\{\begin{array}{l}\;\;\; 112 &= 2 \times 66 - 2 \times 10 \\ \;\;\; 84 &= 84 \end{array}\right.\\$
$\left\{\begin{array}{l}\;\;\; 112 &= 112 \\ \;\;\; 84 &= 84 \end{array}\right.\\$
Donc la somme d’argent de Mohamed est 102 dh et celle d’Ali est 66 dh.

Exercice 6

Le point K est le milieu du segment [MN], donc :
$x_K = \frac{x_M + x_N}{2}$ et $y_K = \frac{y_M + y_N}{2}\\$
$x_K = \frac{3 + (-1)}{2}$ et $y_K = \frac{2 + 6}{2}\\$
$x_K = \frac{2}{2} = 1$ et $y_K = \frac{8}{2} = 4\\$
Alors K(1;4) est le milieu de [MN].
a) Coordonnées du vecteur $\overrightarrow{MN}$
$\overrightarrow{MN} = (x_N - x_M; y_N - y_M)\\$
$\overrightarrow{MN} = (-1 - 3; 6 - 2)\\$
$\overrightarrow{MN} = (-4; 4)\\$
b) Distance MN
$MN = \sqrt{(x_N - x_M)^2 + (y_N - y_M)^2}\\$
$MN = \sqrt{(-4)^2 + 4^2}\\$
$MN = \sqrt{16 + 16}\\$
$MN = \sqrt{32}\\$
$MN = 4\sqrt{2}\\$
Équation réduite de la droite (MN) est de la forme : $y = mx + p\\$
Calculons m :
$m = \frac{y_M - y_N}{x_M - x_N}\\$
$m = \frac{2 - 6}{3 + 1}\\$
$m = \frac{-4}{4} = -1\\$
Donc : $y_{(MN)} = -x + p\\$
Calculons p avec M(3,2) appartenant à (MN) :
$2 = -3 + p\\$
$2 + 3 = p\\$
$p = 5\\$
Finalement, l’équation de (MN) est :
$y_{(MN)} = -x + 5\\$
$(\Delta) \perp (MN)$ signifie que :
$m_{(\Delta)} \times m_{(MN)} = -1 \\$
$m_{(\Delta)} = \frac{-1}{m_{(MN)}} = \frac{-1}{-1} = 1 \\$
Donc l’équation réduite de $(\Delta)$ est :
$y_{(\Delta)} = x + p \\$
$(\Delta)$ par le point K(1;4)
Alors : $4 = 1 + p \\$
$p = 3 \\$
Finalement, $y_{(\Delta)} = x + 3 \\$
Dans ce cas la droite $(\Delta)$ est la médiatrice de segment [MN].

Exercice 7

a) $f$ est une fonction linéaire
Alors : $f(x) = ax\\$
Donc $a = \frac{f(x)}{x} = \frac{f(-4)}{-4} = \frac{-1}{-4} = \frac{1}{4}\\$
Donc $f(x) = \frac{1}{4}x\\$
b) On a $f(x) = \frac{1}{4}x\\$ et $f(-8) = \frac{1}{4} \times (-8) = \frac{-8}{4} = -2 \\$
c) G(b;3) un point de (D) c’est à dire que :
$f(b) = 3 \\$
et on a $f(b) = \frac{1}{4}b \\$
Alors $\frac{1}{4}b = 3 \\$
Alors $b = 3 \times 4 \\$
Alors $b = 12 \\$
a) g est une fonction affine donc $g(x) = ax + b\\$
Calculons b :
On a : $g(x) = 2x + b\\$ et $g(0) = 2\\$
Donc $2 = 2 \times 0 + b\\$
Alors $b = 2\\$
Finalement, $g(x) = 2x + 2\\$
b) On a : $g(x) = 2x + 2\\$
et $g(x) = 0\\$
$2x + 2 = 0\\$
$2x = -2\\$
$x = -1\\$
Donc l’antécédent de 0 par g est -1.

Vous pouvez consulter et télécharger la correction complète en cliquant sur le lien ci-dessous :

Télécharger La correction en PDF

Correction vidéo expliquée – Très bientôt

La correction en vidéo de l’ Examen Régional Mathématiques 2024 – 3APIC Tanger Tetouan Al Hoceima sera bientôt disponible. Restez connectés pour une explication détaillée et des conseils pratiques pour mieux comprendre les réponses !

Abonnez-vous à notre chaîne YouTube

Abonnez-vous à notre chaîne YouTube et activez la cloche de notification pour recevoir toutes nos prochaines vidéos, y compris la correction vidéo expliquée de l’examen régional SVT 2024.

🔔 Abonnez-vous ici

Modal title

Modal title

Correction Examen Régional Mathématiques 2024 - 3APIC Tanger Tetouan Al Hoceima