Angles inscrits et angles au centre

I – Rappel de propriétés importantes :

1/ Propriété 1 :

∗ La somme des mesures des angles d’un triangle est égale à 180°
$\widehat{ABC} + \widehat{ACB} + \widehat{BAC} = 180°$
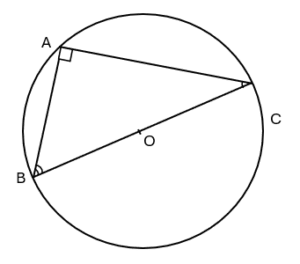
angles inscrits et angles au centre propriété 1

∗ L’angle $\widehat{BOC}$ est plat c’est à dire $\widehat{BOC} = 180°$

∗ Si le triangle $ABC$ est inscrit dans un cercle de diamètre $(BC]$ , alors le triangle $ABC$ est rectangle en $A$ ⇒ $\widehat{BAC} = 90°$

∗ Si l’un des côtés d’un triangle est un diamètre de con cercle circonscrit, alors ce triangle est rectangle au sommet opposé à ce côté.

2/ Propriété 2 :

Une angle complète est égale à 360°

une angle complète est égale à 360°

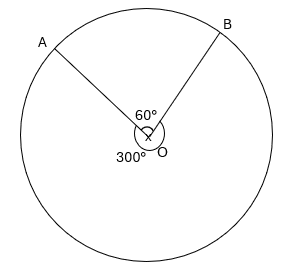
On a $\widehat{AOB} + \widehat{AOB} = 360°\\$
$\widehat{AOB} = 360° - \widehat{AOB}\\$ $\widehat{AOB} = 300°\\$

3/ Propriété 3 :

Dans un triangle équilatéral, les trois angles sont égaux à 60°

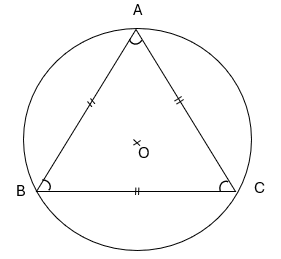
triangle équilatéral, les trois angles sont égaux
$\widehat{ABC} + \widehat{ACB} = \widehat{BAC} = 60°\\$

4/ Propriété 4 :

Dans le triangle isocèle $OBC\\$

triangle isocèle OBC

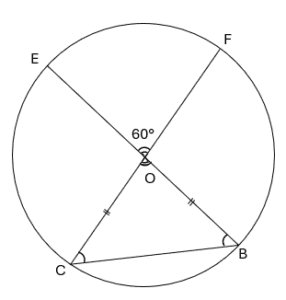
On a :

∗ $OB = OC\\$ car sont deux rayons.

∗ $\widehat{OBC} = \widehat{OCB}$ car sont les angles de la base.

∗ Les angles opposés par le sommet sont égaux $\widehat{BOC} = \widehat{EOF}$

5/ Propriété 5 :

Deux droites parallèles et une sécante.

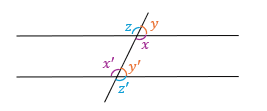
deux droite parallèle et une sécante

$(D) // (D')$ et $(Δ)$ sécante.

$x = x'$ car sont deux angles alternes internes.

$z = z'$ car sont deux angles alternes externes.

$y = y'$ car sont deux angles correspondantes.

6/ Activité globale :

On considère la figure suivante :

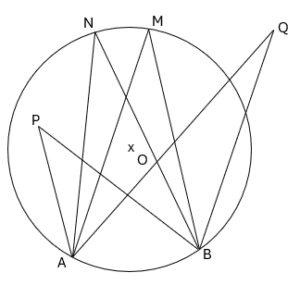
angles inscrits et angles au centre activité globale

Déterminer les angles dont le sommet est sur le cercle et ces deux côtés coupent le cercle en deux points (cet angle s’appelle inscrit).
Déterminer les angles dont le sommet est le centre du cercle (cet angle s’appelle angle au centre).
Déterminer les angles sui ne sont ni inscrit, ni au centre.
Déterminer un angle inscrit et angle au centre associé (c’est à dire interceptent le même arc). Que remarquez vous ?
Déterminer deux angles inscrits qui interceptent le même arc. Que remarquez vous ?

Solution :

Les angles inscrits sont : $\widehat{ANB}$ , $\widehat{AMB}$ , $\widehat{MAB}$ , $\widehat{MNB}$ , $\widehat{NBM}$ et $\widehat{NAM}$ …
Les angles au centre sont : $\widehat{AOB}$ , $\widehat{BOM}$ , $\widehat{MON}$ , $\widehat{NOA}$ , $\widehat{MOA}$ et $\widehat{NOB}$
Les angles $\widehat{APB}$ et $\widehat{AOB}$ ne sont ni inscrit, ni au centre.
L’angle $\widehat{AMB}$ est inscrit et $\widehat{AOB}$ est au centre associé car ils interceptent le même arc $\overset{\large\frown}{AB}\\$
On remarque $\widehat{AOB} = 2\widehat{AMB}$
Les deux angles $\widehat{NBM}$ et $\widehat{NAM}$ sont inscrits interceptent le même arc $\overset{\large\frown}{MN}\\$
On remarque que : $\widehat{NAM} = 2\widehat{NBM}$

II – Angle inscrit :

1/ Définition 1 :

Un angle inscrit dans un cercle est un angle dont le sommet est sur le cercle et dont les côtés coupent le cercle en deux points.

⇒ Figure géométrique :

$(𝒞)$ cercle de centre $O$ , $A$ , $M$ et $C$ trois points du cercle

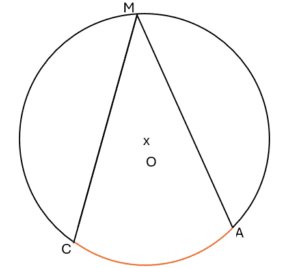
angle inscrit figure géométrique

L’angle $\widehat{AMC}$ est inscrit intercepte l’arc $\overset{\large\frown}{AC}\\$

2/ Cas particulier :

On considère la figure suivante tel que $(AC)$ est une tangente au cercle (𝒞) au point $A$ .

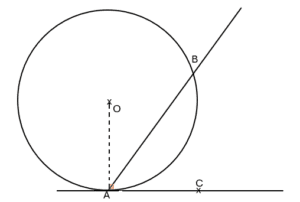
angle inscrit figure géométrique cas particulier.png

L’angle $\widehat{BAC}$ est angle inscrit.

Il intercepte l’arc $\overset{\large\frown}{AB}\\$

III – Angle au centre :

1/ Définition 1 :

Un angle au centre est un angle dont le sommet est le centre du cercle et intercepte un arc dans le cercle.

2/ Exemple :

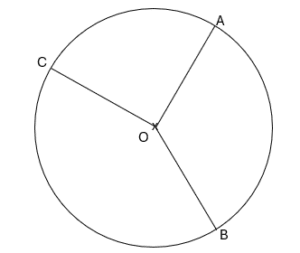
angle au centre exemple

⇒ L’angle $\widehat{AOB}$ est angle au centre intercepte l’arc $\overset{\large\frown}{AB}$

⇒ L’angle $\widehat{AOC}$ est angle au centre intercepte l’arc $\overset{\large\frown}{AC}$

IV – Propriétés :

1/ Angle inscrit et angle au centre associé :

a- Prédéfinition :

Un angle au centre est associé à un angle inscrit s’ils interceptent le même arc.

b- Propriété 1 :

La mesure de l’angle au centre est égale au double de celle de l’angle inscrit qui intercepte le même arc.

∗ Exemple :

On considère la figure suivante :

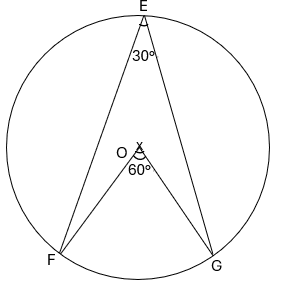
exemple propriété 1 angle inscrit et angle au centre

L’angle $\widehat{FOG}$ est au centre et l’angle $\widehat{FEG}$ est inscrit et interceptent le même arc $\overset{\large\frown}{FG}$

Donc $\widehat{FOG} = 2 \widehat{FEG}\\$

et $\widehat{FEG} = \frac{1}{2} \widehat{FOG}\\$

c- Cas particulier :

$(𝒞)$ cercle de centre $O$ ,

$(AT)$ est tangente du cercle au point $A$ .

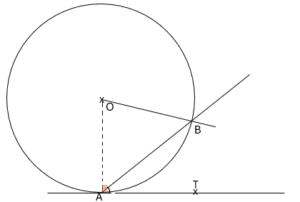
cas particulier

∗ L’angle $\widehat{BAT}$ est inscrit

∗ L’angle $\widehat{AOB}$ est au centre et interceptent le même arc $\overset{\large\frown}{AB}$

Donc $\widehat{AOB} = 2 [latex]\widehat{BAT}$ et $\widehat{BAT} = \frac{1}{2} \widehat{AOB}\\$

2/ Deux angles inscrits interceptant le même arc :

a- Propriété 2 :

Deux angles inscrits interceptent le même arc ont même mesure (isométriques).

∗ Exemple :

Dans la figure suivante :

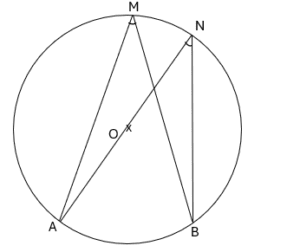
deux angles inscrits interceptent le même arc exemple.png

On a $\widehat{AMB}$ et $\widehat{ANB}$ sont deux angles inscrits qui interceptent le même arc $\overset{\large\frown}{AB}$

Donc $\widehat{AMB} = \widehat{ANB}$

b- Cas particulier :

$(𝒞)$ cercle de centre $O$ ,

$(AT)$ tangente du cercle au point $A$ .

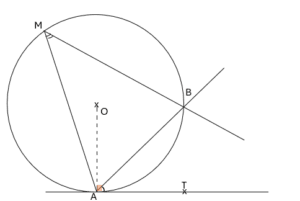
deux angles inscrits interceptent le même arc cas particulier

Les angles $\widehat{BAT}$ et $\widehat{BMA}$ sont inscrits interceptent le même arc $\overset{\large\frown}{AB}$

Donc $\widehat{BAT} = \widehat{BMA}$

∗ Remarque :

⇒ L'arc $\overset{\large\frown}{AB}$ qui ne contient pas le point $M$ s'appelle la petite arc $\widehat{AOB} < 180°$

⇒ L'arc $\overset{\large\frown}{AB}$ qui contient le point $M$ s'appelle la grande arc $\widehat{AOB} > 180°$

Modal title

Modal title

Angles inscrits et angles au centre