Calcul numérique : développement et factorisation
Développement et factorisation
I – Rappel vocabulaire :
1/ Expression algébrique :
Exemples :
A=2x^4 + \frac{2}{3}x^2 - \sqrt3 x +1 \\ B=(2x^2 + 3)(-4x-1)
2/ Expression numérique :
Exemples :
C = 2\sqrt7 + \frac{1}{2} - 11,5 + 17 \\ D=(2\sqrt3 - \frac{11}{3})(11 - \frac{\sqrt5}{2\sqrt7} +1) \\
3/ Somme algébrique :
Exemples :
E = 3x^2 + x\sqrt3 -11\\ F= \sqrt3 x^5 - 4x^3 + 2x^2 - \frac{1}{2}x + \sqrt7 \\
4/ Réduire (simplifier) une expression algébrique :
Exemples :
G = 3x^2 - 2x + 4 -5x^2 + 1 + 7x + x^3\\ \;\;\;\;= x^3 + 3x^2 - 5x^2 - 2x + 7x + 4 + 1\\ \;\;\;\;= x^3 - 3x^2 + 5x + 5\\ H = 3x - 2x^3 + 2x + x^3 - 11 - 5x + 7\\ \;\;\;\;= -2x^3 + x^3 + 3x + 2x - 5x - 11 + 7\\ \;\;\;\;= -x^3 - 4\\
II – Développement et factorisation :
1/ Activité :
ABCD et AEFD deux rectangles tel que : AB = k , AE = a , BE = b 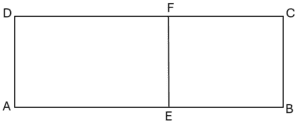 1)Calculer l’air de chacun des rectangles ABCD et AEFD et EBCF. 2)Déduire que : k \times (a+b) = k \times a + k \times b
1)Calculer l’air de chacun des rectangles ABCD et AEFD et EBCF. 2)Déduire que : k \times (a+b) = k \times a + k \times b
Solution :
1) L’air du rectangle AEFD est : S_1 = AE \times AD = k \times a L’air du rectangle EBCF est : S_2 = EF \times EB = k \times b L’air du rectangle ABCD est : S = AD \times AB = k \times (a+b) 2) L’air du rectangle ABCD est la somme des airs des rectangles AEFD et EBCF donc : S = S_1 + S_2 Alors : k \times (a+b) = k \times a + k \times b
2/ Développement :
a- Définition :
b- Règle 1 :
Exemples :
A = 2x(x + 4)\\ \;\;\;\;= 2x \times x + 2x \times 4 \\ \;\;\;\;= 2x^2 + 8x\\ B = (-3x - 5) \times (-4x)\\ \;\;\;\;= -3x \times (-4x) - 5x \times (-4x) \\ \;\;\;\;= 12x^2 + 20x\\ C = 3x(2x^2 - x + 2) -5(3x^2 + 4x - 5)\\ \;\;\;\;= 6x^3 - 3x^2 + 6x - 15x^2 - 20x + 25 \\ \;\;\;\;= 6x^3 - 3x^2 - 15x^2 + 6x - 20x + 25\\ \;\;\;\;= 6x^3 - 18x^2 - 14x + 25\\
b- Règle 2 :
Exemples :
A = (3\sqrt2 - 1)(2 + \sqrt2)\\ \;\;\;\;= 3\sqrt2 \times 2 + 3\sqrt2 \times \sqrt2 - 1 \times 2 - 1 \times \sqrt2 \\ \;\;\;\;= 6\sqrt2 + 3 \times 1 - 2 - \sqrt2 \\ \;\;\;\;= 6\sqrt2 - \sqrt2 +6 - 2\\ \;\;\;\;= 5\sqrt2 + 4\\
B = (2 - x)(3x + 1)\\ \;\;\;\;= 2 \times 3x + 2 \times 1 - x \times 3x - x \times 1 \\ \;\;\;\;= 6x + 2 - 3x^2 - x \\ \;\;\;\;= -3x^2 + 6x - x + 2\\ \;\;\;\;= -3x^2 + 5x + 2\\ C = 3x(2x + 1) + (3x - 2)(x+7)\\ \;\;\;\;= 6x^2 + 3x + 3x^2 + 21x - 2x - 14 \\ \;\;\;\;= 6x^2 + 3x^2 + 3x + 21x - 2x - 14 \\ \;\;\;\;= 9x^2 + 22x - 14\\
3/ Factorisation :
a- Définition :
b- Règle :
b- Remarque importante :
Pour factoriser une expression algébrique, on cherche un facteur commun, après on simplifie l’intérieur des parentheses.
Exemples :
→ Cas 1 : Facteur commun sans parenthèses : A = 2\sqrt3 x - \sqrt6 x^2\\ \;\;\;\;= 2\sqrt3 x - \sqrt2 \times \sqrt3 x^2 \\ \;\;\;\;= \sqrt3 x (2- \sqrt2 x) \\ B = 3x^2 - 9x\\ \;\;\;\;= 3x \times x - 3x \times x \\ \;\;\;\;= 3x(x - 3) \\ → Cas 2 : Facteur commun avec parenthèses : C = (2x + 1)(5 - x) - (2x + 1)(7x + 3)\\ \;\;\;\;= (2x + 1) [(5 - x) - (7x + 3)] \\ \;\;\;\;= (2x + 1) (5 - x - 7x - 3) \\ \;\;\;\;= (2x + 1)(2 - 8x) \\ D = (x + 3)^2 + 2x(x + 3) - (x + 3)\\ \;\;\;\;= (x + 3)(x + 3) + 2x(x + 3) - (x + 3) \times 1 \\ \;\;\;\;= (x + 3)(x + 3 + 2x - 1) \\ \;\;\;\;= (x + 3)(3x + 2) \\
→ Cas 3 : Factorisation double :
E = 7(x - 1) + 2x^2 - 2x\\ \;\;\;\;= 7(x - 1) + 2x(x - 1) \\ \;\;\;\;= (x - 1)(7 + 2x) \\
F = -4x^2 + 2x + (-2x^3 + x^2)\\ \;\;\;\;= 2x(-2x + 1) + x^2(-2x + 1) \\ \;\;\;\;= (1 - 2x)(2x + x^2) \\
III – Identités remarquables :
1/ Propriétés :
2/ Exemples :
→ Identités remarquables et développement : A = (x + 1)^2\\ \;\;\;\;= (x^2 + 2 \times x \times 1 + 1^2 \\ \;\;\;\;= x^2 + 2 \times x + 1\\ B = (2x + 3)^2\\ \;\;\;\;= (2x)^2 + 2 \times 2x \times 3 + 3^2 \\ \;\;\;\;= 4x^2 + 12x + 9\\
3/ Exercice d’application :
1-Développer et simplifier : A = (2x + 1)^2 - (3x + 5)(3x - 5) \\ B = (7 - 2x)^2 + 4x(1-x) \\ 2-Factoriser ce qui suit : C = 25x^2 - 4 + (5x - 2)(5x + 7) \\ D = 9x^2 - 6x + 1 + 5x(3x - 1) \\