Calcul trigonométrique
Calcul trigonométrique
I – Les rapports trigonométriques d’un angle aigu :
1/ Vocabulaire :
ABC est un triangle rectangle en A.
On considère l’angle \widehat{ABC}

∗ Remarques :
⇒ De même pour l’angle \widehat{ABC}, le côté adjacent est AC et le côté opposé est AB.
⇒ Les deux angles \widehat{ABC} et \widehat{ACB} sont aigus c’est à dire 0° < \widehat{ABC}< 90°
⇒ L’hypoténuse est le plus grand côté dabs un triangle rectangle.
2/ Définitions :
∗ Le rapport \frac{AB}{BC} s’appelle le cosinus de l’angle \widehat{ABC} symbolisé par \cos\widehat{ABC}\\
\cos\widehat{ABC} = \frac{côté \, adjacent \, de \, l'angle \widehat{ABC}}{hypoténus} = \frac{AB}{BC}
∗ Le rapport \frac{AC}{BC} s’appelle le sinus de l’angle \widehat{ABC} symbolisé par \sin\widehat{ABC}\\
\sin\widehat{ABC} = \frac{côté \, opposé \, de \, l'angle \widehat{ABC}}{hypoténus} = \frac{AC}{BC}
∗ Le rapport \frac{AC}{AB} s’appelle la tangente de l’angle \widehat{ABC} symbolisé par \tan\widehat{ABC}\\
\tan\widehat{ABC} = \frac{côté \, opposé \, de \, l'angle \widehat{ABC}}{côté \, adjacent \, de \, l'angle \widehat{ABC}} = \frac{AC}{AB}
∗ Exemple :
ABC est un triangle rectangle en A, tel que AB = 3 \; cm et AC = 4 \; cm et BC = 5 \; cm
Calculer les rapports trigonométriques de l’angle \widehat{ABC} et l’angle \widehat{ACB}
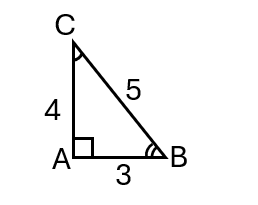
∗ \cos\widehat{ABC} = \frac{AB}{BC} = \frac{3}{5} = 0,6
∗ \sin\widehat{ABC} = \frac{AC}{BC} = \frac{4}{5} = 0,8
∗ \tan\widehat{ABC} = \frac{AC}{AB} = \frac{4}{3}
∗ \cos\widehat{ACB} = \frac{AC}{BC} = \frac{4}{5} = 0,8
∗ \sin\widehat{ACB} = \frac{AB}{BC} = \frac{3}{5} = 0,6
∗ \tan\widehat{ACB} = \frac{AB}{AC} = \frac{3}{4} = 0,75
∗ Exercice d’application :
ABC est un triangle, tel que AB = 2 \; cm, AC = 2\sqrt3 \; cm et BC = 4 \; cm
- Montrer que ABC est un triangle rectangle.
- Calculer les rapports trigonométriques de \widehat{ABC}.
- Calculer les rapports trigonométriques de \widehat{ACB}
3/ L’emploi de la calculatrice dans le calcul trigonométrique :
- En employant la calculatrice, calculons les valeurs approchés des rapports trigonométrique de \alpha = 30°.
On a \cos30° ≈ 0,86\\\sin30° = \frac{1}{2} = 0,5\\\tan30° ≈ 0,57 - En employant la calculatrice, trouvons les valeurs de l’angle \alpha dont les rapports trigonométriques sont respectivement :
On a \cos\alpha_{1} = 0,5\\\sin\alpha_{2} = \frac{\sqrt2}{2}\\\tan\alpha_{3} = 1
∗ En touchant les boutons :
Shift + cos on trouve \alpha_{1} = 60°\\
Shift + sin on trouve \alpha_{2} = 45°\\
Shift + tan on trouve \alpha_{3} = 45°\\
II – Des relations entre les rapports trigonométriques d’un angle aigu :
1/ La relation entre le cosinus et le sinus d’un angle droit :
a- Propriété 1 :
On a : 0 < \cos\alpha < 1 et 0 < \sin\alpha < 1\\
\cos^2\alpha + sin^2\alpha = 1
∗ Remarques :
⇒ \cos^2\alpha + sin^2\alpha = 1 ⇒ \left\{\begin{array}{l}\;\;\;\cos^2\alpha = 1 - \sin^2\alpha\\ \;\;\; \sin^2\alpha = 1 - \cos^2\alpha\end{array}\right.
⇒ C’est à dire si on sait le \cos\alpha(\sin\alpha), on peut calculer le \sin\alpha(\cos\alpha)
⇒ On écrit \cos^2\alpha = (\cos x)^2 pas \cos x^2
b- Exemple :
\alpha est mésure d’un angle aigu tel que \cos\alpha = \frac{2}{3}
Calculons \sin\alpha
⇒ On sait que \sin^2\alpha + \cos^2\alpha = 1
\sin^2\alpha + (\frac{2}{3}) = 1\\\sin^2\alpha + \frac{4}{9} = 1\\\sin^2\alpha = 1 - \frac{4}{9} = \frac{5}{9}\\
Donc \sin^2\alpha = \sqrt\frac{5}{9} Car \sin\alpha > 0\\
Alors \sin\alpha = \frac{\sqrt5}{3}
c- Exercice d’application :
Calculer :
A= 2\cos^2 x+ 3\sin^2 x- 1\\B= (\cos x + \sin x)^2 + (\cos x - \sin x)^2\\C= \sin^4 x - \sin^2 x + \cos^2 x - cos^4 x\\D= \cos^4 x + 2\cos^2 x \sin^2 x + sin^4 x\\
2/ La relation entre cosinus et sinus et tangente d’un angle droit :
a- Propriété 2 :
∗ Remarques :
1) \left\{\begin{array}{l}\;\;\;\sin x = 1 - \tan x \times \cos x\\ \;\;\; \cos x = \frac{\sin x}{\tan x}\end{array}\right.
2) \alpha angle aigu, on a \tan\alpha > 0
b- Exemples :
- x mesure d’angle droit tel que \tan x = 2\sqrt2\\
On a \tan x = \frac{\sin x}{\cos x} Donc 2\sqrt2 = \frac{\sin x}{\cos x}\\
C’est à dire \sin x = 2\sqrt2 \cos x\\
Or \sin^2 x + \cos^2 x = 1\\
(2\sqrt2 \cos x)^2 + \cos^2 x = 1\\
8\cos^2 x + \cos^2 x = 1\\
9\cos^2 x = 1\\
\cos^2 x = \frac{1}{9}\\
\cos x = \sqrt\frac{1}{9} car \cos x > 0\\
Alors \cos x = \frac{1}{3} - x mesure d’angle aigu tel que \sin x = \frac{\sqrt5}{3}\\
Calculons \tan x\\
⇒ Calculons d’abord \cos x\\
On a \cos^2 x + sin^2 x = 1\\
⇒ \cos^2 x + (\frac{\sqrt5}{3})^2 = 1\\
⇒ \cos^2 x + \frac{5}{9} = 1\\
⇒ \cos^2 x = 1 - \frac{5}{9} = \frac{4}{9}\\
⇒ \cos x = \sqrt\frac{4}{9} car \cos x > 0\\
⇒ Alors \cos x = \frac{2}{3}\\
On a \tan x = \frac{\sin x}{\cos x} = \frac{\frac{\sqrt5}{3}}{\frac{2}{3}} = \frac{\sqrt5}{3} \times \frac{3}{2}\\
3/ Les rapports trigonométriques de deux angles complémentaires :
a- Propriété 3 :

\cos x = \sin y\\\sin x = \cos y\\\tan x = \frac{1}{tan y}
b- Exemples :
∗ \sin 70° = \cos 20°\\
∗ \cos 30° = \sin 60°\\
∗ \sin 80° = \cos 10°\\
∗ \cos 45° = \sin 45°\\
∗ \tan 15° = \frac{1}{\tan 75°}\\
∗ \tan 11° = \frac{1}{\tan 79°}\\
c- Exercice d’application :
Calculer :
A= \cos 5° + 2\sin^2 22° - \sin 85° + 2\sin^2 68°\\B= \cos^2 14° + \cos^2 28° + \cos^2 76° + \cos^2 62°\\C= 5\sin^2 34° + 3\cos^2 11° + 5\sin^2 56° + 3\cos^2 79°\\
4/ Angles particuliers :
| x | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| \sin x | 0 | \frac{1}{2} | \frac{\sqrt2}{2} | \frac{\sqrt3}{2} | 1 |
| \cos x | 1 | \frac{\sqrt3}{2} | \frac{\sqrt2}{2} | \frac{1}{2} | 0 |
| \tan x | 0 | \frac{\sqrt3}{2} | 1 | \sqrt3 | Indéfini |
∗ Exemples :
D= \sqrt2\cos 45° + \sin^2 30° + \sin^2 60° + \sqrt3\tan 30°\\D= \sqrt2 \times \frac{\sqrt2}{2} + (\frac{1}{2})^2 + (\frac{\sqrt3}{2})^2 + \sqrt3 \times \frac{\sqrt3}{3}\\D= \frac{2}{2} + \frac{1}{4} + \frac{3}{4} + \frac{3}{3}\\D= 1 + \frac{4}{4} + 1\\D= 2 + 1D= 3\\
∗ Relations supplémentaires :
⇒ Démonstration :
∗ \frac{1}{1 + \tan^2 x} = \frac{1}{1 + (\frac{\sin x}{\cos x})^2} = \frac{1}{1 + \frac{\sin^2 x}{\cos^2 x}} = \frac{1}{\frac{\cos^2 x + \sin^2 x}{\cos^2 x}} = \frac{\cos^2 x}{\cos^2 x + \sin^2 x} = \frac{\cos^2 x}{1} = \cos^2 x\\
∗ \frac{tan^2 x}{1 + \tan^2 x} = \frac{(\frac{\sin x}{\cos x})^2}{1 + (\frac{\sin x}{\cos x})^2} = \frac{\frac{\sin^2 x}{\cos^2 x}}{1+ \frac{sin^2 x}{cos^2 x}} = \frac{\frac{\sin^2 x}{\cos^2 x}}{\frac{cos^2 x + \sin^2 x}{cos^2 x}} = \frac{\sin^2 x}{\cos^2 x + \sin^2} = \frac{\sin^2 x}{1} = \sin^2 x