Equation d’une droite

I – L’équation réduite d’une droite :

1/ Définition :

Dans le plan rapporté à un repère orthonormé chaque droite admet une équation réduite de la forme : $y = mx + p$ ∗ m : est appelé le coefficient directeur (ou la pente) de la droite.∗ p : est appelé l’ordonnée à l’origine.

2/ Exemples :

a- Exemple 1 :

∗ $(D) : 2x - 3$ est l’équation réduite de la droite $(D)$ de pente $m = 2$ et d’ordonnée à l’origine $p = -3$

∗ $(Δ) : y = -x$ est l’équation réduite de la droite $(Δ)$ de pente $m = -1$ et d’ordonnée à l’origine $p = 0$

b- Exemple 2 :

On considère la droite $(D)$ tel que :

(D) : 2y + 3x - 1 = 0

On a $2y + 3x - 1 = 0$ on isole $y$

2y = -3x + 1\\

y = \frac{-3x + 1}{2}\\

(D) : y = -\frac{3}{2}x + \frac{1}{2}

C’est l’équation réduite de la droite $(D)$ de pente $m = \frac{-3}{2}$ et l’ordonnée à l’origine $p = \frac{1}{2}$

c- Exemple 3 : Construction d’une droite définie par son équation réduite :

On considère la droite $(D) : y = -2x + 3$ pour construire la droite $(D)$ , il suffit de déterminer deux points différentes de cette droite.

On prend par exemple :

$x = 0$ donc : $y = -2 \times 0 + 3 = 3$

$x = 1$ donc : $y = -2 \times 1 + 3 = -2 + 3 = 1$

On considère le tableau suivant :

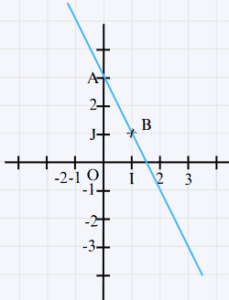
exemple equation d une droite

$x$	$0$	$1$
$y$	$3$	$1$
$M(x;y)$	$A(0;3)$	$B(1;1)$

3/ Cas particulier :

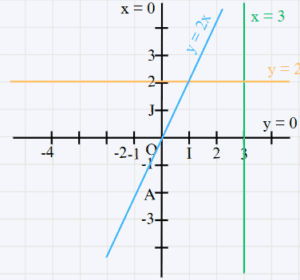
cas particulier equation d une droite

∗ L’équation de l’axe des abscisses est $y = 0$

∗ L’équation de l’axe des ordonnées est $x = 0$

∗ L’équation de la droite parallèle à l’axe des abscisses (horizontale) et passante par le point $M(a;b)$ est : $y = b$

∗ L’équation de la droite parallèle à l’axe des ordonnées (verticale) et passante par le point $M(a;b)$ est : $x = a$

∗ L’équation de la droite passante par le l’origine du repère s’écrit sous la forme $y = mx$ (l’ordonnée à l’origine est nulle)

3/ Remarques importantes :

Un point appartient à une droite si et seulement si ses coordonnées vérifient l’équation de la droite.
Exemple :
Soient $(D) : y = 2x - 3$ et $A(2;1)$
On a $2x_{A} - 3 = 2 \times 2 - 3 = 4 - 3 = 1 = y_{A}$
Alors $A \in (D)$
Soient les points $A(a;y_{A})$ et $B(a;y_{B})$ l’équation de la droite $(AB)$ est $x = a$
Soient les points $A(x_{A};b)$ et $B(x_{B};b)$ l’équation de la droite $(AB)$ est $y = b$

II – Détermination de l’équation d’une droite :

1/ Pente d’une droite définie par deux points :

a- Propriété 1 :

Si $A(x_{A};y_{A})$ et $B(x_{B};y_{B})$ deux points tel que $x_{A} ≠ x_{B}$

Donc la pente de la droite $(AB)$ est :

m = \frac{y_{B} - y_{A}}{x_{B} - x_{A}}

⇒ Remarque :

m = \frac{Différence\; des\; ordonnées}{Différence\; des \;abscisses}

En gardant l’ordre.

b- Exemple :

On considère $A(-1;-3)$ et $B(-4;0)$

La pente de la droite $(AB)$ est :

m = \frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{0-(-3)}{-4-(-1)} = \frac{3}{-3} = -1

2/ Détermination de l’équation réduite d’une droite définie par deux points :

⇒ Déterminons l’équation réduite de la droite $(AB)$ tel que : $A(1;-2)$ et $B(-2;3)$

∗ L’équation réduite de la droite $(AB)$ s’écrit sous la forme : $(AB) : y = mx + p$

On a $m = \frac{y_{B} - y_{A}}{x_{B} - x_{A}} = \frac{3 - (-2)}{-2 - 1} = \frac{5}{-3} = -\frac{5}{3}$

Donc $(AB) : y = -\frac{5}{3}x + p$

∗ Détermination de p

On a $A ∈ (AB)\\$

Donc $y_{A} = -\frac{5}{3}x_{A} + p\\$

-2 = -\frac{5}{3} \times 1 + p\\

-2 = -\frac{5}{3} + p\\

p = -2 + \frac{5}{3} = \frac{-6 + 5}{3} = -\frac{1}{3}\\

Alors $(AB) : y = -\frac{5}{3}x + \frac{1}{3}$

3/ Détermination de l’équation réduite d’une droite définie par sa pente et un point :

Déterminons l’équation réduite de la droite $(Δ)$ de pente 3 et qui passe par le point $E(2;-1)$

∗ On a l’équation réduite de la droite $(Δ)$ s’écrit sous la forme $(Δ) : y = 3x + p$

∗ Détermination de p :

On a : $E ∈ (Δ)\\$

Donc $y_{E} = 3x_{A} + p\\$

Donc $-1 = 3 \times 2 + p \\$

Donc $-1 = 6 + p \\$

Donc $p = -1 - 6 = -7 \\$

Alors l’équation réduite de la droite $(Δ)$ est : $(Δ) : y = 3x - 7$

4/ Exercice d’application :

Soient $A(1;1)$ et $B(2;-1)$

Montrer que l’équation réduite de la droite $(AB)$ est $y = -2x + 3$

III – Parallélisme et orthogonalité de deux droites :

1/ Condition de parallélisme de deux droites :

a- Propriété 2 :

Soient $(D)$ et $(Δ)$ deux droites tel que :

$(D) : y = mx + p$ et $(Δ) : y = m'x + p'$

∗ $(D) // (Δ)$ est équivalente à $m = m'$

Autrement dit : Deux droites sont parallèles si et seulement si ils ont la même pente.

b- Exemple :

On considère les deux droites :

$(D_{1}) : y = -2x + 1$ et $(D_{2}) : y = -2x + 5$

On a : $(D_{1}) // (D_{2})$ car ils ont même pente -2

c- Exercice d’application :

On considère la droite $(D) : y = 2x - 1$

Est ce que $A(-1;1) \in (D)$
Déterminer l’équation réduite de la droite $(Δ)$ passante par $A$ est parallèle à $D$

2/ Condition d’orthogonalité de deux droites :

a- Propriété 3 :

Soient $(D)$ et $(Δ)$ deux droites tel que :

$(D) : y = mx + p$ et $(Δ) : y = m'x + p'$

∗ $(D) \perp (Δ)$ est équivalente à $m \times m' = -1$

Autrement dit : Deux droites sont perpendiculaire si et seulement si le produit de leurs pentes est égale à -1

b- Exemple :

On considère les deux droites :

$(D) : y = -\frac{2}{3}x + 1$ et $(D') : 2y - 3x + 8 = 0$

On a : $2y - 3x + 8 = 0\\$

⇒ $2y = 3x - 8\\$

⇒ $y = \frac{3x - 8}{2}\\$

Alors $(D') : y = \frac{3}{2}x - 4$

On a $\frac{3}{2} \times \frac{-2}{3} = -1$

Donc $(D) \perp (D')$

c- Exercice d’application :

On considère la droite $(D) : y = -4x + 3$

Montrer que $A(0;-1) \notin (D)$
Déterminer l’équation réduite de la droite $(Δ)$ passante par le point A et perpendiculaire à $(D)$
On considère la droite $(D') : x - 4y - 1 = 0$
Montrer que : $(D) \perp (D')$

Modal title

Modal title

Equation d’une droite