Equations et inéquations

I – Equations du premier degré à une inconnue :

1/ Définition :

2/ Exemples :

Toutes les égalités 2x + 3 = 0 et \sqrt2x - \frac{1}{2} = 0 et -7x - 5 = 4 et 2x + 8 = \sqrt3x + 1 s’appelle des équations du premier degré à une inconnue x

∗ Remarque :

→ Résoudre une équation c’est trouver toutes les valeurs possibles de l’inconnue qui vérifient l’équation (s’ils existent).

→ Chacune de ces valeurs est appelée solution de l’équation.

3/ Résolution d’une équation du premier degré à une inconnue :

a- Règle :

b- Cas et techniques de résolution :

Cas 1 : Equation de type ax + b = 0

1. L’équation -3x + 4 = 0 est respectivement équivalente à -3x = -4
   x = \frac{-4}{-3} ⇒ x = \frac{4}{3}
   Dans cette équation admet une unique solution \frac{4}{3}
2. L’équation 5(x + 1) = 2x - 1 est respectivement équivalente à 5x + 5 = 2x - 1
   5x - 2x = - 1 - 5
   3x = -6
   x = \frac{-6}{3} = -2
   Dans cette équation admet une unique solution -2
3. L’équation 2x + 5 = 2(x + 1) + 3 est respectivement équivalente à
   2x + 5 = 2x + 2 + 3
   2x - 2x = 5 - 5
   0x = 0
   Donc tous les nombres réels sont solutions de cette équation.
4. L’équation 3(2x - 1) = 6x + 7 est respectivement équivalente à
   6x - 3 = 6x + 7
   6x - 6x = 7 + 3
   0x = 10
   Ce qui est impossible
   Donc cette équation n’admet pas de solution.

Cas 2 : Equation de type (ax + b)(cx + d) = 0

∗ propriété : Le produit nul

Les solutions de l’équation (ax + b)(cx + d) = 0

Sont les solutions des équations ax + b = 0  et cx + d = 0

1. L’équation (x + 1)(2x - 3) = 0  est respectivement équivalente à
   x + 1 = 0 ou 2x - 3 = 0
   x = -1 ou 2x = 3
   x = -1 ou x = \frac{3}{2}
   Donc cette équation admet deux solutions -1 et \frac{3}{2}
2. L’équation x^2 - 7x = 0 est respectivement équivalente à
   x(x - 7) = 0
   x = 0 ou x - 7 = 0
   x = 0 ou x = 7
   Donc cette équation admet deux solutions 0 et -7

Cas 3 : Equation fractionnaires

∗ Règle : 

1. L’équation \frac{2x + 1}{5} - 2 = \frac{x - 1}{3} est respectivement équivalente à
   \frac{3(2x + 1) - 30}{15} = \frac{5(x - 1)}{15}
   6x + 3 - 30 = 5x - 5
   6x - 5x = -5 -3 +30
   x = 22
   Dans cette équation admet une unique solution.

Cas 4 : Equation de type x^2 = a

→ Remarque :

Pour résoudre ce type d’équation

on rappelle l’identité 3 :
a^2 - b^2 = (a - b)(a + b)\\
∗ propriété : Les solutions d’équation x^2 = a 

– Si a = 0, l’équation admet une unique solution 0

– Si a > 0, l’équation admet deux solutions \sqrt{a} et -\sqrt{a}

– Si a < 0, alors cette équation n’admet pas de solution.

1. L’équation x^2 + 12 = 2 est respectivement équivalente à
   x^2 = 2 - 12
   x^2 = -10
   Donc cette équation n’admet pas de solution.
2. L’équation (2x - 1)^2 - 9 = 0 est équivalente à
   (2x - 1)^2 - 3^2 = 0
   (2x - 1 - 3)(2x - 1 + 3) = 0
   (2x - 4)(2x + 2) = 0
   2x - 4 = 0 ou 2x + 2 = 0
   2x = 4 ou 2x = -2
   x = \frac{4}{2} = 2 ou x = \frac{-2}{2} = -1
   Donc cette équation admet deux solutions -1 et 2

Cas 5 : Equation avec factorisation

Equation avec factorisation, Si on a facteur commun avec identité remarquables

1. L’équation 2x(x + \sqrt2) - \sqrt3(x + \sqrt2) = 0 est respectivement équivalente à
   (x + \sqrt2)(2x - \sqrt3) = 0
   x + \sqrt2 = 0 ou 2x - \sqrt3 = 0
   x = -\sqrt2 ou x = \frac{\sqrt3}{2}
   Donc cette équation admet deux solutions -\sqrt2 et \frac{\sqrt3}{2}

Cas 6 : Equation avec développement 

Résolution d’une équation avec développement si on a les parenthèses et pas de facteur commun.

1. L’équation x(x + 3) = x^2 - 15 est respectivement équivalente à
   x^2 + 3x = x^2 -15
   x^2 + 3x - x^2 = -15
   x = \frac{-15}{3} = -5
   Donc cette équation admet une unique solution -5

II – Résolution des problèmes :

1/ Mise en équation de problèmes :

a- Règle :

2/ Exemple :

La somme des âges de Aziz, de sa mère et de sa grand-mère est 90 ans .

L’âge de la grand-mère est le double de l’âge de la mère et l’âge de Aziz est tiers de celui de sa mère.

Quel est l’âge de chacun ?

⇒ Solution :

1. Choix de l’inconnue :
   Soit x l’âge de la mère
2. Mise en équation :
   ∗ L’âge de la mère est x
   ∗ L’âge de la grand-mère est 2x car c’est le double de l’âge de la mère.
   ∗ L’âge de Aziz est \frac{x}{3} car c’est le tier de la mère.
   Et puisque leurs âges est 90 ans, alors l’équation est : x + 2x + \frac{x}{3} = 90
3. Résolution de l’équation =
   L’équation x + 2x + \frac{x}{3} = 90 est respectivement équivalente à
   \frac{3x + 6x + x}{3} = \frac{270}{3}
   10x = 270
   x = \frac{270}{10} = 27
   Donc la solution de cette équation est 27
4. Retour au problème :
   On a 27 + 2 \times 27 + \frac{27}{3} = 27 + 54 + 9 = 90
   Donc la solution est vraie
   ∗ L’âge de la mère est 27 ans
   ∗ L’âge de la grand-mère est 54 ans
   ∗ L’âge de Aziz est 9 ans

III – Inéquations du premier degré à une inconnue :

1/ Définition :

∗ Remarque :

→ Résoudre une inéquation, c’est trouver toutes les valeurs de x qui vérifient l’inégalité.

2/ Exemples :

∗ Les inégalité 2x + 5 < 0 et \sqrt2x - 7 + b ≥ 0 et 3x + 7 > \frac{2}{3}x - 14

Sont des inéquations du premiers degré à une inconnue x

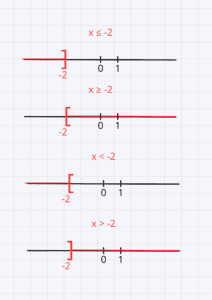
3/ Représentation des solutions d’une inéquation sur une droite graduée :

∗ On représente l’écriture x < a sur la droite par la partie rouge

a ne fait pas partie des réels x qui vérifient x < a le crochet est orienté dans le sens opposé des solutions.

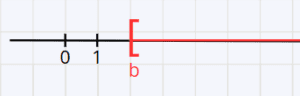
∗ On représente l’écriture x ≥ b sur la droite par la partie rouge

b fait partie des réels x qui vérifient x ≥ b le crochet est orienté dans le sens des solutions.

4/ Résolution des inéquations :

Cas 1 : Si a > 0

Alors les solutions de l’inéquation est ax + b < 0 est x < \frac{-b}{a} (On change pas le symbole)

→ L’inéquation 4x - 5 ≤ 2x + 3 est respectivement équivalente à
4x - 2x ≤ 3 + 5
2x ≤ 8
x ≤ \frac{8}{2}
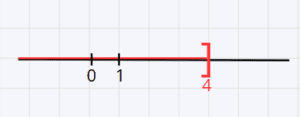
x ≤ 4

Donc tous les nombres réels inférieurs ou égaux à 4 sont solutions de cette inéquation

Cas 2 : Si a < 0

Alors les solutions de l’inéquation ax + b < 0 sont x > \frac{-b}{a} ou inverse le symbole.

→ L’inéquation 2x - 6 > 7x - 1 est respectivement équivalente à
2x - 7x > -1 +6
-5x > 5
x > \frac{5}{-5}
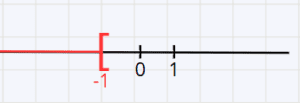
x > -1
Donc tous les nombres réels strictement inférieur à -1 sont solutions de cette inéquation.

Cas 3 : inéquations n’admettent pas de solutions

→ L’inéquation \frac{2x - 5}{3} - \frac{x + 1}{2} ≥ \frac{x}{6} est respectivement équivalente à
\frac{2(2x - 5) - 3(x + 1)}{6} ≥ \frac{x}{6}
4x - 10 - 3x - x ≥ x
4x - 3x - x ≥ 10 + 3
0 ≥ 13
Ce qui est impossible
Donc cette inéquation n’admet pas de solution.

Cas 4 : inéquations admettent infinité de solution

→ L’inéquation 5(2x - 1) - 7x < 3(x + 1) est respectivement équivalente à
10x - 5 - 7x ≥ 3x + 3
10x - 7x - 3x ≥ 3 + 5
0 ≥ 8
Qui est vrai
Donc tous les nombres réels sont solutions de cette inéquation.

5/ Problème et inéquations :

a- Règle :

∗ Remarque :

Lorsque on emploie au problème des expressions comme (ai moins – au plus – moins que – plus que – meilleur que – maximal – minimal …) alors on utilise les inéquations.

b Exemples :

Une agence de location de voitures propose deux tarifs :

– Tarif A : un forfait de 60 DH plus 0,20 DH par kilomètre parcouru.

– Tarif B : 0,8 DH par kilomètre parcouru.

A partir de quelle distance (en km) le tarif A est plus avantageux (moins chèr) pour le client ?

⇒ Solution :

1. Choix de l’inconnue :
   Soit x la distance parcouru par le client.
2. Mise en inéquation :
   ∗ Pour le tarif A, le client doit payer (en DH) 60 + 0,2x
   ∗ Pour le tarif B, le client doit payer (en DH) 0,8x
   Le tarif A est plus avantageux que tarif B signifie que 60 + 0,2 x ≤ 0,8x
3. Résolution de l’inéquation :
   L’inéquation 60 + 0,2 x ≤ 0,8x est respectivement équivalente à
   0,2x - 0,8x ≤ -60
   -0,6x ≤ -60
   (car -0,6 < 0) x ≥ \frac{-60}{-0,6}
   x ≥ 100
4. Retour au problème :
   A partir de 100 km, le tarif A est plus avantageux que le tarif B