Fonctions linéaires et Fonctions affines

I – Fonctions linéaires  :

1/ Définition :

2/ Exemples :

a- Exemple 1 :

f, g et h sont des fonctions linéaires définies par : f(x) = \frac{1}{3}x, g(x) = 0x, h(x) = -\sqrt{5}x

→ f fonction linéaire de fonction \frac{1}{3}

→ g fonction linéaire de fonction 0

→ h fonction linéaire de fonction -\sqrt5

b- Exemple 2 :

f fonction linéaire définie par : f(x) = 2x

1. Calculer f(0), f(-1), f(\sqrt3)
2. Calculer l’image de 3 par f (c’est à dire f(3))
3. Calculer le nombre d’image -8 par la fonction f

Solution :

1. ∗ f(0) = 2 \times 0 = 0
   ∗ f(-1) = 2 \times -1 = -2
   ∗ f(\sqrt3) = 2 \times \sqrt3 = 2\sqrt3
2. On a f(3) = 2 \times 3 = 6
   Donc l’image de 3 par la fonction f est 6
3. Résolvons l’équation f(x) = -8 l’équation f(x) = -8 est respectivement équivalente à
   2x = -8\\
   x = \frac{-8}{2} = -4\\
   Donc : f(-4) = -8\\
   Donc le nombre d’image -8 par f est -4

3/ Propriété : coefficient d’une fonction linéaire :

a- Propriété 1 :

b- Exemple :

On considère la fonction linéaire tel que : f(2) = 6

Déterminons l’expression de la fonction f.

∗ On a f fonction linéaire donc f(x) = ax et son coefficient est : a = \frac{f(2)}{2} = {6}{2} = 3

D’où : f(x) = 3x

4/ Représentation graphique d’une fonction linéaire :

a- Propriété 2 :

b- Exemple :

g est une fonction linéaire définie par :

1. Calculer g(3)
2. Construire la présentation graphique de la fonction g dans un repère orthonormé (O,I,J)

Solution :

1. On a g(x) = \frac{-2}{3}x\\
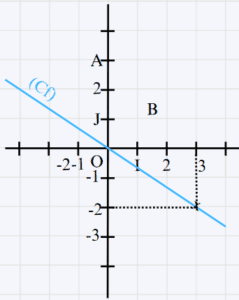
   Donc (3) = \frac{-2}{3} \times 3 = -2
2. On a g(3) = -2 et g linéaire donc la représentation graphique de la fonction g est une droite qui passe par les points O(0;0) et A(3;-2)
   

c- Remarques importantes :

1. Le point M(x;y) appartient à la représentation graphique d’une fonction linéaire f signifie que f(x) = y
2. Pour Déterminer l’image d’un nombre b par une fonction linéaire f graphiquement, on construit la droite verticale passante par b qui coupe (Cf) la représentation graphique de la fonction f en un point d’ordonnée C, Donc f(b) = c
3. Pour déterminer le nombre d’image C par une fonction linéaire f graphiquement, on construit la droite horizontale passante par C qui coupe (Cf) en un point d’abscisse C donc f(C) = b
4. f(x) = ax fonction linéaire, donc l’équation de la droite (Δ) la représentation graphique de la fonction f est : (Δ) : y = ax

5/ Exercice d’application :

f est une fonction linéaire définie par : f(x) = -2x

1. Est-ce que les points A(-1;5) et B(3;-6) appartient à (Cf)
2. Tracer (Cf)

II – Fonctions affines  :

1/ Définition :

2/ Exemples :

a- Exemple 1 :

f(x) = x - 3 et g(x) = 5 et h(x) = \frac{-3}{2}x + 1

→ f fonction affine de coefficient 1.

→ g fonction affine de coefficient 0.

→ h fonction affine de coefficient-\frac{3}{2}.

b- Exemple 2 :

g fonction affine tel que g(x) = 2x - 4

1. Calculer g(0) et g(1)
2. Calculer l’image de 2 par la fonction g
3. Déterminer le nombre d’image 6 par la fonction g

Solution :

1. On a : g(0) = 2 \times 0 - 4 = -4\\
   g(1) = 2 \times 1 - 4 = 2 - 4 = -2\\
2. On a g(2) = 2 \times 2 - 4 = 4 - 4 = 0\\
3. Résolvons l’équation g(x) = 6\\
   L’équation g(x) = 6 est respectivement équivalente à
   2x - 4 = 6\\
   2x = 6 + 4\\
   2x = 10\\
   x = \frac{10}{2} = 5\\
   Alors : g(5) = 6\\
   Le nombre d’image 6 par la fonction g est 5

3/ Propriété : coefficient de la fonction affine :

a- Propriété 3 :

>

b- Exemple :

f une fonction affine tel que :

f(0) = 3 et f(1) = 5

Déterminons l’expression de la fonction f

∗ On a f est une fonction affine

Donc f(x) = ax + b

Son coefficient est a = \frac{f(1) - f(0)}{1 - 0} = \frac{5 - 3}{1} = 2

Donc f(x) = 2x + b

Déterminons b

On a : f(0) = 3

Donc : 2 \times 0 + b = 3

D’où : b = 3

Alors : f(x) = 2x + 3

4/ Représentation graphique d’une fonction affine :

a- Propriété 4 :

>

b- Exemple :

On considère la fonction affine : f(x) = 2x + 4

Traçons dans un repère orthonormé (O,I,J) (Cf)la représentation graphique de la fonction f

On a : f(0) = 2 \times 0 + 4 = 4

(Cf) la représentation graphique de la fonction f est la droite (AB) tel que : A(0;4) et B(-2;0)

c- Remarques importantes :

1. Le point M(x;y) appartient à la représentation graphique de la fonction affine f signifie que : f(x) = y
2. Les méthodes graphiques pour déterminer les images et les nombres dont on connait leurs images restent valables pour une fonction affine.
3. f(x) = ax + b fonction affine donc f(0) = b et l’équation de la droite (Δ) représentation graphique de f est : (Δ) : y = ax + b
4. ∗ Intersection de (Cf) avec l’axe des abscisses ⇒ On résonne l’équation  f(x) = 0   ⇒  A(x;0)\\
   ∗ Intersection de (Cf) avec l’axe des ordonnées  ⇒ On calcule f(0) ⇒ B(0;f(0))
5. La fonction f(x) = a est une fonction affine de coefficient 0 (une fonction constante) et sa représentation graphique est la droite passante par le point A(0;a) et parallèle à l’axe des abscisses.

4/ Exercice d’application :

f et g deux fonctions tel que :

f(x) = ax et g(x) = 2x + b

1. Déterminer a et b tel que :
   f(x-1) = 3 et g(0) = 5
2. Calculer f(2) et g(-1)
3. Déterminer le nombre d’image -4 par la fonction f
4. Déterminer le nombre d’image 7 par g
5. Tracer (D) et (Δ) les représentations graphiques des fonctions f et g respectivement
6. Déterminer les coordonnées de H point d’intersection de (D) et (Δ) graphiquement et algébriquement.