La Puissance électrique

I – Notion de puissance électrique

1) Expérience

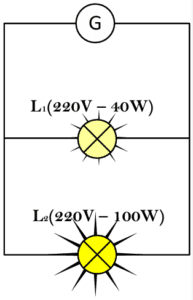
Dans le montage ci-contre, on compare l’éclat des deux lampes L_{1} et L_{2}\\

L_{1} porte les indications (220V - 40W) et L_{2} (220V - 100W)

2) Observation et interprétation

• La lampe L_{2} brille plus que L_{1} : on dit que L_{2}(100W) est plus puissante que L_{1}(40W).
• 100W et 40W représentent les puissances électriques des deux lampes.

3) Conclusion

• La puissance électrique, notée P, est une grandeur physique qui nous renseigne sur la performance d’un appareil électrique : éclairage, chauffage, mouvement …
• L’unité légale de la puissance est le watt de symbole W.
  • Le milliwatt (mW) : 1 mW = 0,001 W = 10^{-3} W
  • Le kilowatt : 1kW = 10^3 W
  • Le mégawatt : 1 MW = 10^6 W
  • Le gigawatt : 1 GW = 10^9

4) Remarque

Tout appareil électrique porte une plaque signalétique comportant ses caractéristiques nominales :

• Tension nominale U : tension normale d’utilisation.
• Intensité nominale I : est l’intensité du courant qui traverse l’appareil lorsqu’il fonctionne normalement.
• Puissance nominale P : est la puissance électrique qu’il reçoit lorsqu’il est soumis à sa tension nominale.

II – La puissance consommée par un appareil électrique

1) Expérience

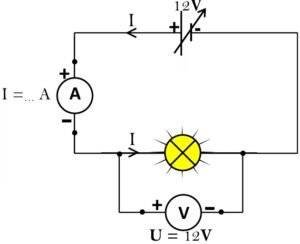
On réalise le circuit électrique ci-dessous en utilisant une lampe L(12V - 25W)\\

On mesure l’intensité I du courant qui traverse la lampe et la tension U entre ses deux bornes, puis on calcule le produit U \times I

2) Observation

Nous remarquons que le produit U \times I est très proche de la puissance nominale de la lampe.

3) Conclusion

La puissance électrique P consommée par un appareil est égale au produit de la tension U entre ses bornes et de l’intensité I du courant qui le traverse.

Cette relation permet de calculer la tension U : U = \frac{P}{I}\\

Cette relation permet de calculer la tension I : I = \frac{P}{U}

4) Remarque

• En courant alternatif, la relation P = U \times I n’est applicable que pour les appareils de chauffage (les appareils qui transforment l’énergie électrique en énergie thermique comme : le four ; fer à repasser ; …). Dans ce cas, on applique la relation :P = U_{eff} \times I_{eff}\\

  Avec :

  U_{eff} la tension efficace en volt (V)\\
  I_{eff} la tension efficace en ampère (A)

• La puissance totale consommée par une installation électrique est égale à la somme des puissances des appareils qui la composent.
  P_{tot} = P_{1} + P_{2} + P_{3} + …
• Pour éviter les pannes de courant, la puissance totale consommée P_{tot} doit être inférieure ou égale à la puissance électrique maximale P_{max} spécifiée pour chaque foyer par l’Agence de distribution de l’électricité.
  P_{tot} ≤ P_{max}\\
  Pour protéger l’installation, on place des coupe-circuits (fusible ou disjoncteur) qui ouvrent le circuit lorsque I_{tot} > I_{max}\\

III – La puissance électrique consommée par un appareil de chauffage

Un appareil qui transforme l’énergie en chaleur (lampe, four électrique, fer à repasser …) est constitué d’un conducteur ohmique de résistance R\\

• Selon la loi d’Ohm : U = R \times I (1)
• Et on sait que : P = U \times I (2)
• A partir des deux relations (1) et (2), on déduit que : P = R \times I \times I = R \times I^2
• La puissance électrique P consommée par un conducteur ohmique de résistance R, traversé par un courant d’intensité I est donnée par la formule suivante :
  P = R \times I^2