Repère dans le plan
Repère dans le plan
I – Les coordonnées d’un point :
1/ Repère orthonormé du plan :
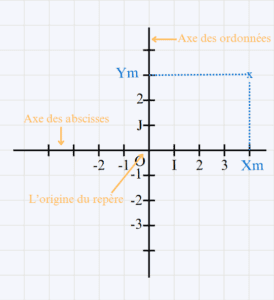
O, I et J trois points du plan tel que :(OI) \perp (OJ) et OI = OJ = 1∗ Le repère (O,I,J) s’appelle repère orthonormé.
On dit que le plan est rapporté à un repère orthonormé (O,I,J).
∗ Le point O est appelé : L’origine du repère.
∗ La droite (OI) est appelé : L’axe des abscisse.
∗ La droite (OJ) est appelé : L’origine des ordonnées.
2/ Les coordonnées d’un point :
a- Définition :
Dans un plan rapporté à un repère orthonormé, pour tout point M, il existe un couple unique de nombres réels (X_{M};Y_{M}) appelé couple de coordonnées du point M.X_{M} : l’abscisse de MY_{M} : l’ordonné de M
Et on écrit : M(X_{M};Y_{M})
b- Exemple :
Le plan est rapporté à un repère orthonormé
Plaçons les points :
A(2 ; -3) ; B(2 ; 4) ; C(-1 ; 2) ; D(-4 ; -2) ; E(0 ; -4) ; F(3 ; 0)
c- Remarques importantes :
∗ (O,I,J) un repère orthonormé, donc O(0 ; 0) et I(1 ; 0) et J(0 ; 1)
∗ Si M un point de l’axe des abscisses donc Y_{M} = 0 et on écrit M(X_{M} ; 0)
∗ Si M un point de l’axe des ordonnées donc X_{M} = 0 et on écrit M(0 ; Y_{M})
3/ Les coordonnées du milieu d’un segment :
a- Définition :
Soit A(X_{M};Y_{M}) et B(X_{M};Y_{M}) deux points du plan.Si M est le milieu du segment [AB], alors :x_{M} = \frac{x_{A} + x_{B}}{2} et y_{M} = \frac{y_{A} + y_{B}}{2}
Et on écrit : M(\frac{x_{A} + x_{B}}{2} ; \frac{y_{A} + y_{B}}{2})
b- Exemple :
Soient A(-2 ; 6) et B(4 ; -8)
Déterminons les coordonnées du point E milieu du segment [AB]
On a : x_{E} = \frac{x_{A} + x_{B}}{2} = \frac{-2 +4}{2} = \frac{2}{2} = 1
Et : y_{E} = \frac{y_{A} + y_{B}}{2} = \frac{6 + (-8)}{2} = \frac{-2}{2} = -1
Donc E(1 ; -1)
c- Exercice d’application :
Dans le plan rapporté à un repère orthonormé, on considère les points :
A(-2 ; 1) et B(2 ; 2) et C(3 ; -2) et D(x ; y)
- Déterminons les coordonnés de E milieu de [AC]
- Déterminons x et y sachant que E est milieu du segment [BD]
II – Les coordonnées d’un vecteur :
1/ Les coordonnées d’un vecteur :
a- Définition :
Dans un repère orthonormé (O,I,J), soit les points A(x_{A};y_{A}) et B(x_{B};y_{B}) les coordonnées du vecteur \overrightarrow{AB} sontx_{B} - x_{A} et y_{B} - y_{A}et on écrit : \overrightarrow{AB}(x_{B} - x_{A} ; y_{B} - y_{A})
b- Exemple :
Soient A(2 ; 3) et B(-1 ; -4) et C(3 ; 2)
∗ Les coordonnées du vecteur \overrightarrow{AB}
On a
\overrightarrow{AB}(x_{B} - x_{A} ; y_{B} - y_{A})\\ \overrightarrow{AB}(-1 -2 ; -4 -3)\\ \overrightarrow{AB}(-3 ; -7)\\∗ Les coordonnées du vecteur \overrightarrow{AC}
On a :
\overrightarrow{AC}(x_{C} - x_{A} ; y_{C} - y_{A})\\ \overrightarrow{AC}(3 - 2 ; 2 - 3)\\ \overrightarrow{AC}(1 ; -1)\\∗ Les coordonnées du point E tel que \overrightarrow{AE}(1 ; 1)
On a :
\overrightarrow{AE}(x_{E} - x_{A} ; y_{E} - y_{A})\\ \overrightarrow{AE}(x_{E} - 2 ; y_{E} - 3)\\Comme \overrightarrow{AE}(1 ; 1)
Donc \left\{\begin{array}{l} x_{E} - 2 = 1\\ y_{E} - 3 = 1 \end{array}\right. ⇒ \left\{\begin{array}{l} x_{E} = 1 + 2 = 3 \\ y_{E} = 1 + 3 = 4 \end{array}\right.
Alors : E(3;4)
2/ Egalité de deux vecteurs :
a- Définition :
b- Exemple :
Soient A(2 ; 3) ; B(-2 ; 4) ; C(-1 ; 2) et D(3 ; 1)
Comparons les vecteurs \overrightarrow{AB} et \overrightarrow{DC}
On a :
\left\{\begin{array}{l} \overrightarrow{AB}(x_{B} - x_{A}; y_{B} - y_{A}) \\ \overrightarrow{DC}(x_{C} - x_{D}; y_{C} -</p> <p>y_{D}) \end{array}\right.\\ \left\{\begin{array}{l} \overrightarrow{AB}(-2 -2; 4 - 3) \\ \overrightarrow{DC}(-1 -3; 2 - 1) \end{array}\right.\\ \left\{\begin{array}{l} \overrightarrow{AB}(-4 ; 1) \\ \overrightarrow{DC}(-4 ; 1) \end{array}\right.\\D’où : \overrightarrow{AB} = \overrightarrow{DC}
c- Exercice d’application :
On considère les points A(2 ; -2) ; B(4 ; -1) ; C(-6 ; -2)
Déterminer le couple des coordonnées du point D tel que ABCD est parallélogramme.
3/ Coordonnées de la somme et différence de deux vecteurs :
a- Définition :
b- Exemple :
Soient \overrightarrow{AB}(3; -1) et \overrightarrow{OD}(2; -4)
∗ On a \overrightarrow{AB} + \overrightarrow{CD}(3 + 2 ; -1 + (-4))
\overrightarrow{AB} + \overrightarrow{CD}(5 ; -5)∗ On a \overrightarrow{AB} - \overrightarrow{CD}(3 - 2 ; -1 - (-4))
\overrightarrow{AB} - \overrightarrow{CD}(1 ; 3)c- Exercice d’application :
On considère les points A(2 ; -1) ; B(3 ; 5) ; D(-3 ; 7) ; C(x ; y) et M(-7 ; 21)
- Déterminer x et y sachant que \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}
- Montrer que \overrightarrow{DM} = \overrightarrow{AB} + \overrightarrow{AD}
4/ Coordonnées du produit d’un vecteur par un nombre réel :
a- Propriété 3 :
b- Exemple :
On considère le vecteur \overrightarrow{AB}(3;-1)
On a : 2\overrightarrow{AB}(2 \times 3 ; 2 \times (-1))
Donc : 2\overrightarrow{AB}(6 ; -2)
Et on a : -4\overrightarrow{AB}(-4 \times 3 ; -4 \times (-1))
Donc : -4\overrightarrow{AB}(-12 ; 4)
c- Exercice d’application :
On considère les points A(2 ; -1) et B(3 ; 5) et C(4 ; 11)
Montrer que les points A, B et C sont alignés.
III – La distance entre deux points :
1/ Propriété 4 :
Alors AB = \sqrt{(x_{B} - x_{A})^2 + (y_{B} - y_{A})^2}
∗ Remarque importante :
Si \overrightarrow{AB}(x,y) alors AB = \sqrt{x^2 + y^2}
2/ Exemple :
Soient \overrightarrow{AB}(3; 4) et E(3; 1) et F(0 ; -2) deux points du plan rapporté à un repère orthonormé.
Calculer AB et EF
∗ Calcul de AB
On a AB = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25}
D’où : AB = 5
∗ Calcul de EF
⇒ Méthode 1 : Propriété 4 :
On a : EF = \sqrt{(x_{F} - x_{E})^2+ (y_{F} - y_{E})^2}
EF = \sqrt{(0 - 3)^2 + (-2 -1)^2} EF = \sqrt{9 + 9} EF = \sqrt{18}D’où : EF = 3\sqrt{2}
3/ Exercice d’application :
Dans un repère orthonormé, on considère les points A(1 ; 5) ; B(3 ; 9) ; C(11 ; 5) et D(9 ; 1)
Montrer que ABCD est un rectangle.