Menu

Statistiques

Statistiques

Statistiques

I – Rappel :

1/ Etude statistique :

Etude d’un phénomène ou d’un caractère qui caractérise les membres d’un groupe.

2/ Population statistique :

C’est l’échantillon ou le groupe qui fait l’objet de l’étude statistique et chaque membre s’appelle individu ou unité statistique.

3/ Caractère :

C’est le phénomène étudié qui est une propriété qu’on peut observer ou mesurer et est de deux types :

a- Caractère quantitatif :

Caractère qu’on peut l’exprimer par des nombres (nombres d’enfants, les notes, âge, poids, longueur…)

b- Caractère qualitatif :

Caractère qu’on ne peut pas l’exprimer par des nombres (sexe, couleur, type de voiture …)

4/ Effectif :

C’est le nombre des unités qui prennent une des valeurs du caractère, on le symbolise par n_{i} (nombre de répétitions)

5/ Effectif total :

C’est la somme de tous les effectifs symbolisé par N

6/ Effectif cumulé :

D’une valeur du caractère est la somme des effectifs de tous les valeurs qui sont inférieure ou égale à cette valeur.

7/ Fréquence :

La fréquence d’une valeur est le quotient de l’effectif de cette valeur par l’effectif total N. f_{i} = \frac{n_{i}}{N}

8/ Fréquence cumulée :

D’une valeur est le quotient de l’effectif cumulé de cette valeur par l’effectif total N

9/ Pourcentage :

Pourcentage est le produit de la fréquence par 100.p_{i} = \frac{Effectif}{Effectif \;total} \times 100 = f_{i} \times 100\\

⇒ Remarques importantes :

→ La somme de toutes les fréquences d’une série statistique est égale à 1.

→ La fréquence cumulée d’une valeur est la somme de la fréquence de cette valeur et des fréquences des valeurs précédentes.

→ On a deux types de série statistiques.

∗ discret : En valeurs si le nombre des valeurs est petit et on les range dans l’ordre croissant.

∗ continu : En classes si le nombre des valeurs est élevé et on les regroupe en classes de même amplitude a ≤ x ≤ b

II – Tableau des effectifs, des effectifs cumulés des fréquences et des fréquences cumulés :

1/ Série statistique discrète en valeur :

Si le caractère est quantitatif et le nombre des valeurs est petit, on les range dans l’ordre croissant.

→ Application 1 :

Le tableau suivant représente une série statistique qui exprime la répartition de 24 adhérent dans un club sportif selon leur âge :

Caractère 12 13 14 15 16
Effectif 5 6 x 8 4
Effectif cumulée 11 24
Fréquence
Fréquence cumulé
  1. La population statistique est 24 adhérent dans un club
  2. L’unité statistique est un adhérent.
  3. Le caractère étudié est l’âge de l’adhérent qui est un caractéristique quantitatif discret.
  4. Le nombre d’adhérents x dont leur âges est 14 ans :
    On a l’effectif total est N = 24\\
    On a : 5 + 6 + x + 8 + 4 = 24\\
    23 + x = 24\\
    x = 24 - 23\\
    x = 1
  5. Remplissons le tableau précédent :
Caractère 12 13 14 15 16
Effectif 5 6 x 8 4
Effectif cumulée 5 11 12 20 24
Fréquence \frac{5}{24} = 0,26 \frac{6}{24} = 0,25 \frac{1}{24} = 0,04 \frac{8}{24} = 0,33 0,17
Fréquence cumulé 0,21 0,46 0,50 0,83 1

6. On a 0,21 + 0,25 + 0,04 + 0,33 + 0,17 = 1\\

Alors la somme de tous les fréquences est égale à 1

7. Représentation graphique :

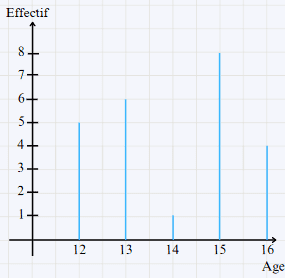
a- Diagramme en bâtons : 

Diagramme en batons (statistiques)

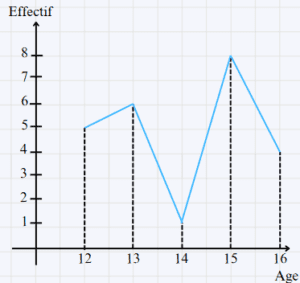
b- Diagramme à ligne brisée : 

(Courbe polygonale)

Diagramme à ligne brisée (statistiques)

→ Application 2 :

Une étude statistique a été menée sur le nombre d’enfants dans 20 familles et a donné les résultats suivants :

2 - 3 - 4 - 3 - 0 - 4 - 3 - 2 - 1 - 1 - 2 - 1 - 0 - 2 - 3 - 4 - 1 - 3 - 0 - 1
  1. Donner le tableau des effectifs et des effectifs cumulées de cette serie.
  2. Calculer la fréquence de la valeur 0
  3. Calculer le pourcentage de la valeur 0
  4. Calculer le pourcentage du nombre de familles dont le nombre d’enfant dépasse 2
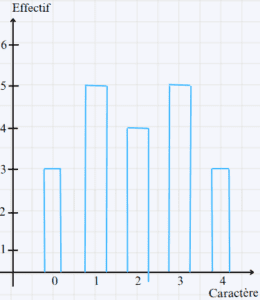
  5. Représenter cette série en colonnes.

Solution :

  1. Le tableau des effectifs et effectifs cumulées
    Caractère : nombre d’enfants 0 1 2 3 4
    Effectif : nombre de familles 3 5 4 5 3
    Effectif cumulée 3 8 12 17 20
  2.  Soit f la fréquence de la valeur 0, donc :
    f = \frac{n}{N} = \frac{3}{20} = 0,15
  3. Le pourcentage de la valeur 0 est :
    p = f \times 100 = 0.15 \times 100 = 15%
  4. Le nombre de familles dont le nombre d’enfants dépasse 2 est : n = 5 + 3 = 8\\
    Donc le pourcentage est : p = f \times 100 = \frac{n}{N} \times 100 = \frac{8}{20} \times 100 = 40%
  5. Diagramme en colonnesDiagramme en colonne (statistiques)

2/ Série statistique en classes :

Si le caractère est quantitatif et le nombre de ses valeurs est élevé, au lieu d’étudier toutes les valeurs, on les regroupe dans des intervalles de même amplitude [a,b[ appelés des classes. et le centre de la classe est \frac{a + b}{2}

→ Application 3 :

Le bilan suivant dans la répartition d’âges des ouvriers dans une ferme.

16 - 26 - 34 - 17 - 22 - 45 - 36 - 27 - 29 - 25 - 19 - 18 - 32 - 42 - 21 - 33 - 35 -  16 - 26 - 34 - 17 - 22 - 38 - 36 - 27 - 29 - 38 - 13 - 18 -  32 - 30 - 39
  1. Déterminer la population de cette série.
  2. Déterminer le caractère étudie et son type.
  3. Compléter le tableau suivant :
    Age en année [10,20[ [20,30[ [30,40[ [40,50[
    Centre de classe
    Effectif : nombre d’ouvriers
  4. Combien d’ouvriers dans la ferme ?
  5. Calculer le pourcentage des ouvriers dont l’âge et inférieur à 20 ans.
  6. Calculer la fréquence de la classe [30,40[
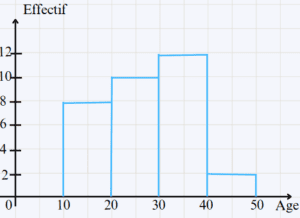
  7. Construire l’histogramme de la répartition des ouvriers de la ferme selon les classes de leurs âges.

⇒ Solution :

  1. La population est les ouvriers de la ferme.
  2. La caractère statistique est l’âge d’ouvrier et c’est une caractère quantitatif continu.
  3. Age en année [10,20[ [20,30[ [30,40[ [40,50[
    Centre de classe \frac{12 + 20}{2} = 15 25 35 45
    Effectif : nombre d’ouvriers 8 10 12 2
  4. Le nombre d’ouvrier dans la ferme est :
    N = 8 + 10 + 12 + 2 = 32
  5. Le nombre d’ouvriers dont l’âge est inférieur à 20 ans est n = 8\\
    Donc leur pourcentage est :
    p = \frac{n}{N} \times 100 = \frac{8}{32} \times = 25%\\
  6. La fréquence f de la classe [30,40[ est :
    f = \frac{n}{N} \times 100 = \frac{12}{32} \times = 0,375\\
  7. Si la répartition est sous forme de classes [a,b[ ou d’intervalles a ≤ x ≤ b, on emploie un histogramme

⇒ Diagramme circulaire :

Convenable pour les caractères qualitatifs.

Un diagramme circulaire est un diagramme qui a la forme d’un disque décomposé en secteurs dont les mesures des angles sont proportionnelles aux effectifs (et également aux fréquences)

Mésure \; de \; l'angle = \frac{Effectif}{Effectif \; total} \times 360°\\ = fréquence \times 360°\\ = \frac{pourcentage}{100} \times 360°

III – Les paramètres de position :

1/ Le mode :

a- Définition :

Le mode d’une série statistique est la valeur du caractère qui a le plus grand effectif.

b- Exemples :

→ Exemple 1 : Regarde Application 1

Caractère 12 13 14 15 16
Effectif 5 6 1 8 4

On a le plus grand effectif est 8 et sa valeur est 15

Donc le mode de cette série est 15

→ Exemple 2 :

Caractère (coefficient) 1 2 3 5
Effectif nombre de matières) 3 2 2 3

Pour cette série, le plus grand effectif est 3, correspondant aux valeurs 1 et 5, donc cette série admet deux modes 1 et 5.

→ Exemple 3 :

Les longueurs de 8 élèves en cm sont :

61 - 68 - 67 - 73 - 66 - 64 - 59 - 70

Existe-t-il une valeur plus fréquente que d’autres dans ces données ?

La réponse est non.

Donc cette série n’admet pas de mode.

∗ Série en classes :

⇒ Définition :

On appelle classe modale d’une série statistique groupées en classe, toute classe qui a le plus grand effectif.

⇒ Exemple :

On considère la série suivante :

Classe [120,130[ [130,140[ [140,150[ [150,160[
Effectif 9 11 12 18

Le plus grand effectif est 18, correspond à la classe [150,160[, donc la classe modale est [150,160[

Remarque : 

Une série statistique ne peut pas avoir un mode (classe modale), comme elle peut avoir plusieurs modes (classes modale)

2/ La moyenne arithmétique :

a- Définition :

La moyenne arithmétique est le rapport de la somme de toutes les produits de chaque valeur (centre de classe) fois son effectif sur l’effectif total. On le note m.

Remarque : 

La moyenne arithmétique m est égale au rapport de la somme de toutes les valeurs sur l’effectif total.

C’est à dire c’est la valeur obtenu si toutes les valeurs du caractère sont égaux.

b- Exemples :

∗ Série en valeurs :

→ Exemple 1 :

Regarde l’application 2 :

On a : m = \frac{(0 \times 3) + (1 \times 5) + (2 \times 4) + (3 \times 5) + (4 \times 3)}{20}\\

m = \frac{0 + 5 + 8 + 15 + 12}{20} = 2

Donc 2 est la moyenne du nombre d’enfants dans chaque famille.

→ Exemple 2 :

On considère la série suivante :

Caractère (coefficient) 1 2 3 5
Effectif (nombre de matières) 3 2 2 3
m = \frac{(1 \times 3) + (2 \times 2) + (3 \times 2) + (5 \times 3)}{10}\\ m = \frac{3 + 4 + 6 + 15}{10} = \frac{28}{10}\\ m = 2,8

∗ Série en classes :

→ Règle :

Si a ≤ x < b est une classe d’une série, alors son milieu est \frac{a + b}{2}∗ Pour calculer la moyenne d’une série statistique en classes, on utilise la définition précédente en remplaçant les valeurs par les centres des classes.

→ Exemple :

Regarde l’application 3 :

Age (années) [10,20[ [20,30[ [30,40[ [40,50[
Centre de classe \frac{10 + 20}{2} = 15 25 35 45
Effectif : nombre d’ouvrier 8 10 12 2
m = \frac{(15 \times 8) + (25 \times 10) + (35 \times 12) + (45 \times 2)}{32}\\ m = 27,5

Alors la moyenne d’âges des ouvriers est 27.5 et cela signifie que si on a supposé que tous les ouvriers, ont le même âge,

L’âge de chaque ouvrier va être 27,5 ans.

3/ La médiane :

a- Définition :

La médiane d’une série statistique est la plus petite valeur d’un caractère dont l’effectif cumulé est supérieur ou égale à la médiane de l’effectif total.

b- Exemples :

∗ Série en valeurs :

Regarde l’application 1 :

Caractère  12 13 14 15 16
Effectif 5 6 1 8 4
Effectif cumulé 5 11 12 20 24
  • La moitié de l’effectif totale est \frac{50}{2} = 25
  • Le premier effectif cumulé supérieur ou égale à 25 est 32, correspond à la classe [140,150[
    Donc la médiane de cette série se trouve dans la classe [140,150[

Remarque : 

On peut dire que 145 (centre de la classe [140,150[) est la médiane de cette série statistique.

c- Autre définition : médiane

La médiane d’une série statistique, dont les valeurs sont ordonnées, est la valeur du caractère qui partage la série en deux parties de même effectif.

→ Cas 1 : effectif total N est impaire

∗ Exemple :

Nombre d’absences pendant 7 jours d’ouvriers d’une société sont : 3 - 1 - 2 - 0 - 4 - 2 - 3

On les range dans l’ordre croissant :

0 - 1 - 2 – 2 – 3 - 3 - 4

Donc la médiane est 2

→ Cas 2 : N est pair

∗ Exemple :

Nombre d’absences pendant 8 jours ordonné :

0 - 1 - 1 - 2 – 3 - 4 - 4 - 5\\

M = \frac{2 + 3}{2} = \frac{5}{2} = 2,5\\

On peut prendre comme médiane tout nombre compris entre 14 et 16 d’où la médiane de cette série est : 2,5

VI – La dispersion :

1/ Définition :

On considère deux série statistiques S_{1} et S_{2} qui ont la même moyenne arithmétique mOn dit que la série S_{1} est moins dispersée que S_{2}. Si les valeurs de S_{1} sont plus proches de m que celles de S_{2}

2/ Exemple :

On considère le tableau suivant :

Devoir D_{1} D_{2} D_{3} 1D_{4}5 D_{5}
Notes de Sabrine 9 14 10 13 14
Notes de Saad 8 16 10 17 9

– Moyenne de Sabrine :

m_{1} = \frac{9 + 14 + 10 + 13 + 14}{5} = \frac{60}{5} = 12\\

– Moyenne de Saad :

m_{2} = \frac{8 + 16 + 10 + 17 + 9}{5} = \frac{60}{5} = 12\\

Donc m_{1} = m_{2}

C’est à dire Sabrine et Saad ont même moyanne.

On remarque que les notes de Sabrine sont plus proches de la moyenne 12 que celle de Saad

On dit que : les notes de Sabrine sont moins dispersés que les notes de Saad.

Copyright 2024, tous droits réservés

contact@profelhamdaoui.com

+212 750-254331