Théorème de Thalès

I – Théorème de Thalès direct :

1/ Activité 1 :

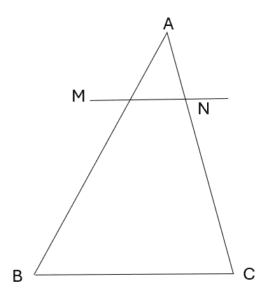
On considère la figure ci-dessous tel que (MN)//(BC)\\

AM = 3 ; AB = 8 ; MN = 1,5 ; AC = 4

Calculer AN et BC

Solution :

On considère le triangle ABC

On a \left\{\begin{array}{l}\;\;\;M ∈ [AB] \\ \;\;\; M ∈ (AC] \end{array}\right. tel que (MN) // (BC)\\

Donc d’après Thalès

On a : \frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}\\

c’est à dire : \frac{AM}{AB} = \frac{AN}{AC} et \frac{AM}{AB} = \frac{MN}{BC}\\

Donc \frac{3}{8} = \frac{AN}{4} et \frac{3}{8} = \frac{1,5}{BC} \\

AN = \frac{3 \times 4}{8} = \frac{3}{2} et BC = \frac{8 \times 1,5}{3} = 4\\

2/ Exemple :

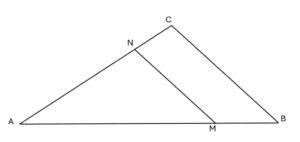
(D) et (Δ) deux droites sécantes en A\\

Soient B et M  deux points de la droite (D) distincts du point A et soient C et N deux points de la droite (Δ) distincts du point A tel que :(MN) // (BC)\\

Dans les trois cas, on a :

Dans tous les cas, on aura

3/ Théorème de Thalès directe :

4/ Application sur le triangle :

a- Propriété 1 :

ABC un triangle
Si \left\{\begin{array}{l}\;\;\;M ∈ (AB) \\ \;\;\; M ∈ (AC) \end{array}\right. tel que (MN) // (BC) Alors
\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}

b- Remarques :

∗ Le théorème de Thalès directe nécessite deux conditions à savoir l’appartenance et parallélisme et donne la triple égalité.

∗ On utilise le Théorème de Thalès directe pour calculer les langueurs.

c- Exemple :

ABC un triangle tel que :

AB = 6 \; cm, AC = 4 \; cm et BC = 5 \; cm

Soit E un point de [AB] tel que AE = 2 \; cm

La parallèle à BC passante par E coupe [AC] en F

1. construire la figure
2. Calculer AF et EF

Solution :

1. La figure :
2. Calcul de AF et EF

On considère le triangle ABC

On a \left\{\begin{array}{l}\;\;\;E ∈ (AB) \\ \;\;\; F ∈ (AC) \end{array}\right. tel que (EF) // (BC)

Donc d’après le Théorème de Thalès directe, On a :

Donc \frac{2}{6} = \frac{AF}{4} et \frac{2}{6} = \frac{EF}{5} \\

AF = \frac{2 \times 4}{6} = \frac{4}{3} et EF = \frac{2 \times 5}{3} = 6 = \frac{5}{3}\\

AF = \frac{4}{3}cm et EF = \frac{5}{3}cm

II – La réciproque du Théorème de Thalès :

1/ Activité 1 :

ABC un triangle tel que AB = 6 et AC = 6

M et N deux points de [AB] et [AC] respectivement tel que : AM = 2 et AN = 3

1. Construire la figure
2. Montrer que \frac{AM}{AB} = \frac{AN}{AC}
3. Montrer que (MN) // (BC)

Solution :

1.  La figure :
2. On a \frac{AM}{AB} = \frac{2}{4} = \frac{1}{2} et \frac{AN}{AC} = \frac{3}{6} = \frac{1}{2}

   Donc \frac{AM}{AB} = \frac{AN}{AC}

3. On considère le triangle ABC

   On a \left\{\begin{array}{l}\;\;\;M\; milieu\; de\; (AB) \\ \;\;\; N\; milieu\; de\; (AC)\end{array}\right.

   Donc d’après la propriété 1 du chapitre triangle et droite parallèles, on a : (MN) // (BC)

2/ Théorème de Thalès réciproque :

3/ Application sur le triangle :

a- Propriété 2 :

ABC un triangle
Si \left\{\begin{array}{l}\;\;\;M ∈ (AB) \\ \;\;\; M ∈ (AC) \end{array}\right. et les points A, M et B et les points de A, N et C ont le même ordre tel que \frac{AM}{AB} = \frac{AN}{AC} Alors (MN) // (BC)

b- Remarques :

1. Le théorème de Thalès réciproque nécessite trois conditions (appartenance + ordre des points + égalité) et donne le parallélisme.
2. On utilise la réciproque du Théorème de Thalès pour prouver le parallélisme.
3. La condition de l’ordre des points sur chaque droite est nécessaire pour appliquer la réciproque de Théorème de Thalès.

c- Exemple 1 :

On considère la figure :

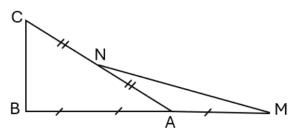
On a \frac{AM}{AB} = \frac{1}{2} et \frac{AN}{AC} = \frac{1}{2}

Donc \frac{AM}{AB} = \frac{AN}{AC}

Et pourtant (MN) et (BC) ne sont pas parallèles,

Car l’ordre des points A, N et C est différent de l’ordre des points A, M et B

d- Exemple 2 :

ABC un triangle tel que AB = 4 \; cm et AC = 6 \; cm

E un point de [AB] tel que : AE = 2 \; cm

F un point de (AC] tel que : AF = 3 \; cm

1. Construire la figure
2. Montrer que (BC) // (EF)

Solution :

1. La figure :
2. On a \frac{AE}{AB} = \frac{2}{4} = \frac{1}{2} et \frac{AF}{AC} = \frac{3}{6} = = \frac{1}{2}

   Donc \frac{AE}{AB} = \frac{AF}{AC}

   On considère le triangle ABC

   On a \left\{\begin{array}{l}\;\;\;E ∈ (AB) \\ \;\;\; F ∈ (AC) \end{array}\right. et les points A, E et B et les points de A, F et C ont le même ordre.

   Et puisque : \frac{AE}{AB} = \frac{AF}{AC}

   Donc d’après le théorème de Thalès réciproque, on a : (BC) // (EF)