Triangles isométriques et triangles semblables

I – Triangles isométriques :

1/ Définition :

Deux triangles isométriques sont des triangles superposables.

2/ Exemple et vocabulaire :

Soient ABC et EFG deux triangles isométriques.

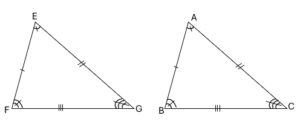
∗ Les côtés correspondants : (homologues)
\left \{ \begin{array}{r c l} & → &[AB] et [EF] deux\; côtés\; correspondants\\ & → & [AC] et [EG] \\ & → & [BC] et [FG] \end{array} \right .
∗ Les angles correspondants : (homologues)
\left \{ \begin{array}{r c l} & → & \widehat{BAC} \;et\; \widehat{FEG} \;deux\; angles\; correspondants\\ & → & \widehat{ABC} \;et\; \widehat{EFG} \\ & → & \widehat{ACB} \;et\; \widehat{EGF} \end{array} \right .

3/ Propriété 1 :

Si deux triangles sont isométriques, alors :

→ Leurs côtés correspondant ont le même longueur.

→ Leurs angles correspondants ont la même mesure.

∗ Exemple :

Dans l’exemple précédent, on a

\left \{ \begin{array}{r c l}AB = EF\\ AC = EG \\ BC = FG \end{array} \right .  ;  \left \{ \begin{array}{r c l}\widehat{ABC} = \widehat{EFG}\\ \widehat{ACB} = \widehat{EGF} \\ \widehat{BAC} = \widehat{FEG} \end{array} \right .

3/ Cas d’isomètre :

∗ Cas 1 : côté + côté + côté (3 côtés)

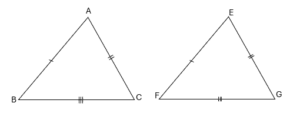
Si on a \left \{ \begin{array}{r c l}AB = EF\\ AC = EG \\ BC = FG \end{array} \right . Alors les triangles ABC et EFG sont isométriques.

∗ Cas 2 : côté + angle entre eux + côté (2 côtés et angle)

Si on a \left \{ \begin{array}{r c l}AB = EF\\ AC = EG \\ \widehat{BAC} = \widehat{FEG} \end{array} \right . Alors les triangles ABC et EFG sont isométriques.

∗ Cas 3 : angle + côté adjacent + angle (2 angles et côté)

Si on a \left \{ \begin{array}{r c l}\widehat{BAC} = \widehat{FEG}\\ AB = EF \\ \widehat{BAC} = \widehat{EFG} \end{array} \right . Alors les triangles ABC et EFG sont isométriques.

∗ Cas 1 :

∗ Cas 2 :

∗ Cas 3 :

II – Triangles semblables :

1/ Définition :

2/ Exemple :

Dans les triangles ABC et EFG

On a : \left \{ \begin{array}{r c l}\widehat{BAC} = \widehat{FEG}\\ \widehat{ABC} = \widehat{EFG} \\ \widehat{ACB} = \widehat{EGF} \end{array} \right . Donc les triangles ABC et EFG sont semblables.

∗ Remarques importantes :

→ Les côtés correspondants (homologues) sont :

\left \{ \begin{array}{r c l}[AB] \;et\;[EF]\\ [AC] \;et\;[EG] \\ [BC] \;et\;[FG] \end{array} \right . mais ne sont pas égaux.

→ Deux triangles isométriques sont semblables mais la réciproque et fausse.

3/ Propriété 2 :

→ Autrement dit :

Si ABC et EFG sont deux triangles semblables (dans cet ordre), alors \frac{AB}{EF} = \frac{AC}{EG} = \frac{BC}{FG} = k
k est appelé rapport de similitude.

∗ Remarques importantes :

→ Dans la figure précédente, on a :
\frac{EF}{AB} = \frac{EG}{AC} = \frac{FG}{BC} = k > 1\\
k s’appelle le rapport de similitude des triangles EFG et ABC dans cet ordre.

– Le triangle EFG est un agrandissement de ABC dont le rapport (coefficient) d’agrandissement est k > 1

→ On a \frac{AB}{EF} = \frac{AC}{EG} = \frac{BC}{FG} = \frac{1}{k} < 1\\

\frac{1}{k} est le rapport de similitude des triangles ABC et EFG

– Le triangle ABC est une réduction de EFG dont le rapport de réduction est \frac{1}{k} < 1

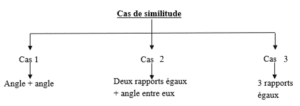
4/ Cas de similitude :

a- Cas 1 :

∗ Exemple :

Dans cette figure, on a :

∗ \widehat{BAC} = \widehat{MAN} car elle sont opposés par le sommet.

∗ \widehat{ABC} = \widehat{AMN} = 90° car elles sont deux angles droits.

Donc d’après le cas 1 de similitude, les triangles \widehat{BAC} et \widehat{AMN} sont semblables.

b- Cas 2 :

→ Autrement dit :

Soient ABC et EFG deux triangles.
Si \left\{\begin{array}{l}\;\;\;\widehat{BAC} = \widehat{FEG}\\ \;\;\; \frac{AB}{EF} = \frac{AC}{EG} \end{array}\right. Alors les triangles ABC et EFG sont semblables.

∗ Exemple :

Dans cette figure, on a :

∗ \widehat{ABC} = \widehat{AMN} car sont deux angles droits.

∗ On a \left\{\begin{array}{l}\;\;\;\frac{AM}{AB} = \frac{4}{8} = \frac{1}{2}\\ \;\;\; \frac{MN}{BC} = \frac{3}{6} = \frac{1}{2} \end{array}\right.\\
\frac{AM}{AB} = \frac{MN}{BC}
Donc d’après le cas 2 de similitude, les deux triangles AMN et ABC sont semblables dont le rapport de similitude est \frac{1}{2}

c- Cas 3 :

Autrement dit :

Soient ABC et EFG deux triangles.
si \frac{AB}{EF} = \frac{AC}{EG} = \frac{BC}{FG}, alors les triangles ABC et EFG sont semblables.

∗ Exemple :

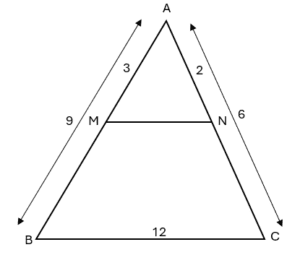
∗ \frac{AB}{AM} = \frac{9}{3} = 3

On a 

∗ \frac{AC}{AN} = \frac{6}{2} = 3

∗ \frac{BC}{MN} = \frac{12}{4} = 3

Donc ∗ \frac{AB}{AM} = \frac{AC}{AN} = \frac{BC}{MN}

Donc d’après le cas 3 de similitude, les deux triangles ABC et AMN sont semblables dont le rapport de similitude est 3.

∗ Remarques :

∗ Deux figures sont semblables s’ils ont la même forme générale et si l’un est l’agrandissement k > 1 ou réduction k < 1 de l’autre.

∗ Le rapport de similitude compare entre deux mesures de même unité, il est utilisé par exemple, pour faire des cartes et des dessins géométriques avec des petites mesures des figues réels.

Par exemple l’échelle 1 \; cm par chaque 100 \; m signifie que chaque cm dans la carte présente 100 \; m dans la réalité.