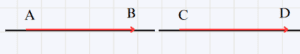Vecteurs et translation
Vecteurs et translation
I – Le vecteur :
1/ Caractéristiques d’un vecteur non nul :
a- Définition :
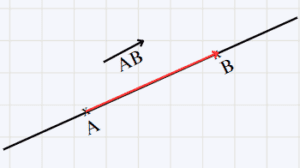
Le couple (A,B) détermine le vecteur \overrightarrow{AB} de caractéristiques :
→ La direction : c’est la droite (AB)
→ Le sens : le sens de la demi droite [AB) c’est à dire de A vers B
→ La norme (module) : la distance AB
– Le point A est l’origine du vecteur \overrightarrow{AB}
– Le point B est l’extrémité du vecteur \overrightarrow{AB}
b- Figure géométrique :
2/ Vecteur nul :
a- Définition :
– Chaque point A détermine un vecteur nul \overrightarrow{AA} noté \overrightarrow{O} et on écrit : \overrightarrow{AA} = \overrightarrow{O}
– Si \overrightarrow{AB} = \overrightarrow{O} alors A = B (c’est à dire les points A et B sont confondus)
→ Remarque :
La norme d’un vecteur nul est zéro, mais la direction et le sens ne pas définis.
3/ L’opposé d’un vecteur :
a- Définition :
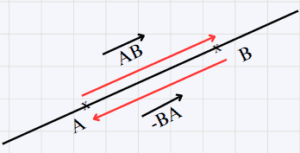
Le vecteur \overrightarrow{BA} s’appelle l’opposé du vecteur \overrightarrow{AB} et on écrit \overrightarrow{AB} = -\overrightarrow{BA}
b- Figure géométrique :
On a \overrightarrow{AB} = -\overrightarrow{BA}
II – Egalité de deux vecteurs :
1/ Définition :
-
- \overrightarrow{AB} et \overrightarrow{CD} ont même direction c’est à dire (AB) // (CD)
- \overrightarrow{AB} et \overrightarrow{CD} ont même sens.
- \overrightarrow{AB} et \overrightarrow{CD} ont même norme c’est à dire AB = CD
→ Remarque :
Même direction signifie que leurs direction sont : soit deux droites strictement parallèles, soit deux droites confondus.
→ Figure géométrique :
On a \overrightarrow{AB} = \overrightarrow{CD}
Premier cas
Deuxième cas
2/ Propriétés importantes :
- \overrightarrow{AB} = \overrightarrow{DC} est équivalente à les segments [AC] et [BD] ont même milieu.
- \overrightarrow{AB} = \overrightarrow{DC} équivalente à ABCD est un parallélogramme.
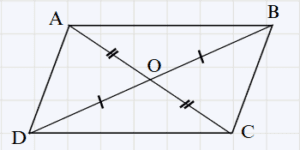
→ Figure géométrique :
ABCD est un parallélogramme.
On a :
- \overrightarrow{AB} = \overrightarrow{DC}
- Les segments [AC] et [BD] ont même milieu.
→ Remarque :
ABCD est un parallélogramme signifie que \left\{\begin{array}{l}\overrightarrow{AB} = \overrightarrow{DC} \\ \overrightarrow{BA} = \overrightarrow{CD} \\ \overrightarrow{AD} = \overrightarrow{DA} \\ \overrightarrow{CB} = \overrightarrow{DC} \end{array}\right.
3/ Exercice d’application :
Soit ABC un triangle
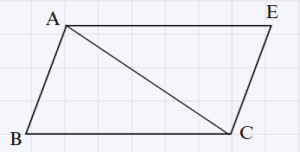
- Construire le point E tel que \overrightarrow{AE} = \overrightarrow{BC}
- Montrer que : \overrightarrow{AB} = \overrightarrow{EC}
Solution :
- On a \overrightarrow{AE} = \overrightarrow{BC}
- On a \overrightarrow{AE} = \overrightarrow{BC}
Donc AECB est un parallélogramme,
Alors \overrightarrow{AB} = \overrightarrow{EC}
III – Somme de deux vecteurs :
1/ Définition :
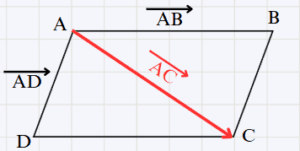
Et on écrit : \overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}
→ Figure géométrique :
ABCD est un parallélogramme.
Donc \overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}
→ Récapitulatif d’un parallélogramme :
ABCD est un parallélogramme, donc :
1 – \left\{\begin{array}{l}\overrightarrow{AB} = \overrightarrow{DC} \\ \overrightarrow{BA} = \overrightarrow{CD} \\ \overrightarrow{AD} = \overrightarrow{BC} \\ \overrightarrow{DA} = \overrightarrow{CB} \end{array}\right. 2 – \left\{\begin{array}{l}\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC} \\ \overrightarrow{BA} + \overrightarrow{BC} = \overrightarrow{BD} \\ \overrightarrow{CB} + \overrightarrow{CD} = \overrightarrow{CA} \\ \overrightarrow{DA} + \overrightarrow{DC} = \overrightarrow{DB} \end{array}\right.
3 – [AC] et [BD] ont même milieu
2/ Relation de Charles :
a- Propriété :
Cette égalité s’appelle Relation de Charles.
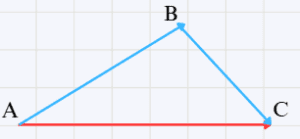
b- Figure :
\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}
c- Exemples :
Simplifions les écritures suivantes :
∗ \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \overrightarrow{AC} + \overrightarrow{AC} = \overrightarrow{AA} = \overrightarrow{O}
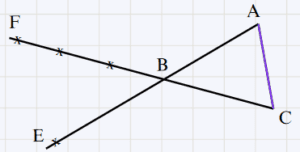
∗ \overrightarrow{AC} - \overrightarrow{BC} + \overrightarrow{BE} = \overrightarrow{AC} + \overrightarrow{CB} + \overrightarrow{BE} = \overrightarrow{AB} + \overrightarrow{BE} = \overrightarrow{AE}
∗ \overrightarrow{AB} + \overrightarrow{ED} + \overrightarrow{BE} + \overrightarrow{DC} = \overrightarrow{AB} + \overrightarrow{BE} + \overrightarrow{ED} + \overrightarrow{DC} = \overrightarrow{AE} + \overrightarrow{EC} = \overrightarrow{AC}
3/ Exercice d’application :
Soit ABC un triangle
- a) Construire le point E tel que \overrightarrow{AC} = \overrightarrow{AE} + \overrightarrow{AB}
b) Construire les points M et N les symétriques respectifs de A et C par rapport à B - Montrer que \overrightarrow{NC} = \overrightarrow{NA} + \overrightarrow{NM}
IV – Produit d’un vecteur par un nombre réel :
1/ Définition :
∗ Si k < 0 alors AM = -k \times AB et \overrightarrow{AM} et \overrightarrow{AB} ont des sens opposé.
∗ Si k = 0 alors A et M sont confondus.
→ Remarque :
\overrightarrow{O} \times \overrightarrow{AB} = \overrightarrow{O} et k \times \overrightarrow{O} = \overrightarrow{O}
2/ Exemples :
ABC un triangle
Construisons les points E et F tels que :
\overrightarrow{AE} = 2\overrightarrow{AB} et \overrightarrow{BF} = \frac{-3}{2}\overrightarrow{BC}
\overrightarrow{AE} = 2\overrightarrow{AB} donc \left\{\begin{array}{l}E ∈ (AB) \\ \overrightarrow{AE} \; et \; \overrightarrow{AB} \; ont \; même \; sens \\ AE = 2 \times AB \end{array}\right.
\overrightarrow{BF} = \frac{-3}{2}\overrightarrow{BC} donc \left\{\begin{array}{l}F ∈ (BC) \\ \overrightarrow{BF} \; et \; \overrightarrow{BC} \; ont \; des \; sens \; opposés \\ BF = \frac{3}{2} \times BC \end{array}\right.
3/ Vecteurs et milieu :
a- Propriété :
→ Remarque :
On utilise souvent \overrightarrow{AM} = \overrightarrow{MB}
4/ Propriétés importantes :
∗ Si \overrightarrow{AC} = k\overrightarrow{AB} alors les points A, B et C sont alignés.
∗ Si \overrightarrow{AB} = k\overrightarrow{MN} alors (AB) // (MN) on dit que les deux vecteurs \overrightarrow{AB} et \overrightarrow{MN} sont colinéaires.
5/ Exercices d’application :
⇒ Exercice 1 :
ABCD un parallélogramme et E un point tel que \overrightarrow{DE} = \frac{2}{3}\overrightarrow{AB}
Montrer que les points D, C et E sont alignés
⇒ Exercice 2 :
Soient ABC un triangle et E et F deux points tel que : \overrightarrow{AE} = \frac{-7}{5}\overrightarrow{BC} et C est le milieu du segment [BF]
Montrer que : (AE) // (CF)
V – La translation :
1/ Activité :
A, B et M trois points du plan
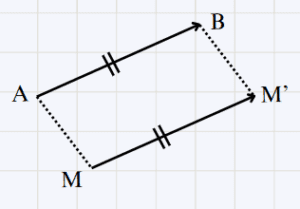
Construire dans chacun des cas le point M' tel que \overrightarrow{MM'} = \overrightarrow{AB}
Cas 1
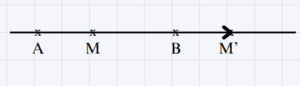
Cas 2
ABM'M est parallélogramme
Dans chacun des cas, on dit que le point M' est l’image du point M par la translation T du vecteur \overrightarrow{AB} (qui transforme A en B)
2/ Définition :
On dit que le point M' est l’image du point M par la translation du vecteur \overrightarrow{AB} (qui transforme A en B) si \overrightarrow{MM'} = \overrightarrow{AB} c’est à dire ABM'M est un parallélogramme.
3/ Propriété caractéristique :
→ Remarque :
Soit T_{\overrightarrow{AB}} la translation de vecteur \overrightarrow{AB} alors, l’image de A pat T est le point B et l’image de B par T est le point C tel que B est le milieu du segment [AC]
4/ Exercice d’application :
ABCD un parallélogramme de centre O
- Construire le point E image de D par la translation de vecteur \overrightarrow{AC}
- Construire F symétrique de D par rapport à A
- Montrer que O est milieu de [EF]
VI – L’image de quelques figures par une translation :
1/ L’image d’une droite :
a- Propriété 1 :
→ Remarque importante :
Pour construire l’image d’une droite par une translation, On construit les images de deux points de cette droite par la translation.
b- Figure géométrique :
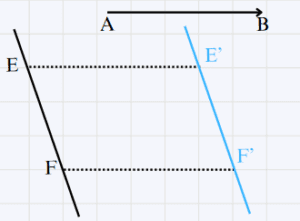
\overrightarrow{AB} un vecteur non nul et (D) droite
construisons (D') image de (D) par la translation de vecteur \overrightarrow{AB}
On a : (D) // (D')
c- Propriété 2 :
On dit que la translation conserve l’alignement des points.
d- Exercice d’application :
ABCD un parallélogramme de centre O
- Construire E image de A par la translation de vecteur \overrightarrow{OD}
- Construire F image de C par la même translation.
- Montrer que les points E, F et D alignés.
2/ L’image d’une demi-droite :
a- Propriété 3 :
b- Figure géométrique :
\overrightarrow{AB} et [EF) demi-droite.
Construisons [E'F') l’image de [EF) par la translation de vecteur \overrightarrow{AB}
3/ L’image d’un segment :
a- Propriété 4 :
On dit que la translation conserve la distance.
b- Figure géométrique :
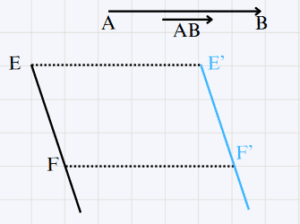
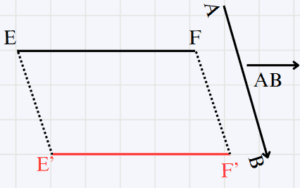
\overrightarrow{AB} vecteur non nul et [EF] un segment.
Construisons [E'F'] l’image de [EF] par la translation de vecteur \overrightarrow{AB}
On a (EF) // (E'F') et EF = E'F'
4/ L’image d’un angle :
a- Propriété 5 :
On dit que la translation conserve la mesure des angles.
b- Figure géométrique :
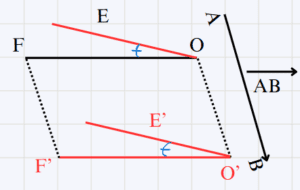
\overrightarrow{AB} vecteur non nul et \widehat{EOF} un angle
Construisons l’angle \widehat{E'O'F'} l’image de l’angle \widehat{EOF} par la translation de vecteur \overrightarrow{AB}
On a : \widehat{EOF} = \widehat{E'O'F'}
5/ L’image d’un cercle :
a- Propriété 6 :
→ Remarque importante :
Pour construire l'image d'un cercle par une translation, on construit l'image du centre par la même translation et on garde le même rayon.
b- Figure géométrique :
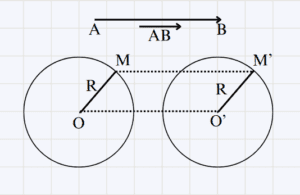
\overrightarrow{AB} un vecteur non nul et 𝒞 un cercle de centre O et de rayon R.
Construisons le cercle 𝒞' image du cercle 𝒞' par la translation du vecteur \overrightarrow{AB}.
6/ Exercice d'application :
Soit ABCD un triangle tel que : AB = 4 \;cm et \widehat{BAC} = 70°
On considère la translation t de vecteur \overrightarrow{AC}
Soient E et F les images respectives des points C et B par la translation t.
- Tracer la figure.
- Montrer que (BC) // (EF).
- Calculer CF
- Calculer \widehat{FCE}